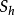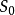擬柱體

定義

所有的頂點都在兩個平行平面內的多面體叫做擬柱體。它在這兩個平面內的面叫做擬柱體的底面，其餘各面叫做擬柱體的側面，兩底面之間的垂直距離叫做擬柱體的高。

擬柱體是指所有的頂點都在兩個平行平面中的多面體。

擬柱體的側面可是是三角形、梯形或平行四邊形。

下面給出一般擬柱體（不包括台塔）體積的計算公式:

其中，h為高，

在高度平行於底面的截面積；

，高度h，就是頂面；

，高度0，就是底面。

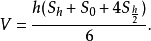
其來源為對不超過三次的多項式，以辛普森積分法求定積分之結果。

一般的柱體、稜台、台塔、球檯等都屬於擬柱體。

在幾何學中，平行六面體是由六個平行四邊形所組成的三維立體。它與平行四邊形的關係，正如正方體與正方形之間的關係；在歐幾里得幾何中這四個概念都允許，但在仿射幾何中只允許平行四邊形和平行六面體。平行六面體的三個等價的定義為：

六個面都是平行四邊形的多面體；

有三對對面平行的六面體；

底面為平行四邊形的稜柱。

長方體（六個面都是長方形）、正方體（六個面都是正方形），以及菱面體（六個面都是菱形）都是平行六面體的特殊情況。

反稜柱（Antiprism）是由兩個相同邊數多邊形平行基底和側面的三角形所組成的一個多面體。反稜柱的對偶多面體是偏方面體（Trapezohedron）。

稜柱是幾何學中的一種常見的三維多面體，指兩個平行的平面被三個或以上的平面所垂直截得的封閉幾何體。

若用於截平行平面的平面數為n，那么該稜柱便稱為n-稜柱。如三稜柱就是由兩個平行的平面被三個平面所垂直截得的封閉幾何體。

在幾何學中，台塔是一種多面體，是透過接和兩個平行的多邊形面，一面作為頂面，另一個邊數是前者的兩倍之多邊形做為底面，然後側面由四邊形和三角形接合所產生的多面體稱為台塔。

若一台塔的面都是正多邊形，那該台塔就屬於詹森多面體。