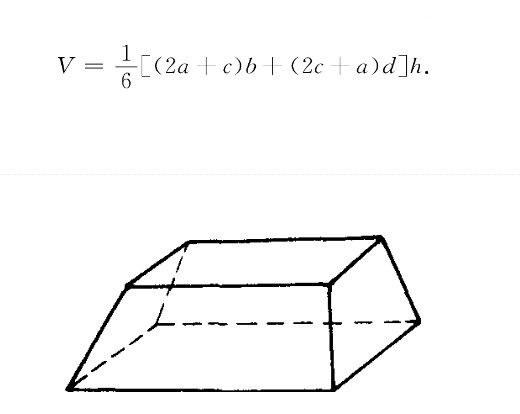
長方台(cuboid frustum)是一種特殊的擬柱體，兩底面都是矩形，並且它們的對應邊平行的擬柱體稱為長方台。
基本介紹
- 中文名：長方台
- 外文名：cuboid frustum
- 所屬學科：數學
- 所屬問題：立體幾何（擬柱體）
- 簡介：一種特殊的擬柱體
基本介紹,長方台展開計算,錐體長方台展開計算,矩形敞口台展開計算,史書記載的長方台體積計算,
基本介紹
兩底面是矩形、且對應邊平行的擬柱體叫長方台。長方台在中國古代稱芻童、盤池、冥谷，並在《九章算術》中給出了它的體積計算公式，其公式是擬柱體體積公式的特例。
圖6中上底長(
)，寬(
)；下底長(
)，寬(
)；高(h)為已給，它的體枳公式是
V芻童=
圖1(如圖1)這兩個矩形的面叫做長方台的底面，如圖中的ABCD和A'B'C'D'，其餘各叫做長方台的側面如ABB'A'、BCC'B'等，兩底面間的距離叫做和長方台的高，如OO'，長方台的各側棱延長後不一定相交於同一點。
擬柱體 所有頂點都在兩個平行的平面內的多面體稱為“擬柱體”。其中平行的兩個多邊形面稱為擬柱體的底面，其餘的面(一般為三角形、平行四邊形或梯形)稱為擬柱體的側面，兩底面之間的距離稱為擬柱體的高，通過高的中點且平行於底面的截面稱為擬柱體的中截面。設
分別為擬柱體兩底面和中截面的面積，h為它的高，則其體積是
【例1】鑄造一個長方台ABCD-A1B1C1D1如圖，上，下底面是互相平行的矩形，相對側面與底面的夾角相等，已知AB =4，BC=2，A1B1=3，B1C1=1，高h=2(單位：米)，求該長方台的體積。
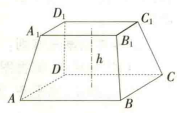圖2解法1 (不是稜台——切法) 如圖切兩次。
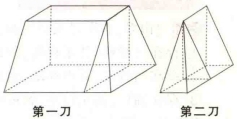圖3
解法2 （用擬柱體計算體積的萬能公式）
V擬柱體
長方台展開計算
長方台有錐體長方台和非錐體長方台之分，錐體長方台錐線匯交於一點，非錐體長方台又稱敞口矩形台，錐線不匯交一點， 須分別求出各面放樣尺寸作出展開圖。下面分別加以介紹。
錐體長方台展開計算
圖4所示為錐體長方台，已知尺寸為A、B、H及h。計算式:
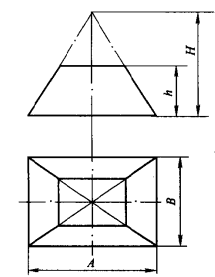圖4（a）
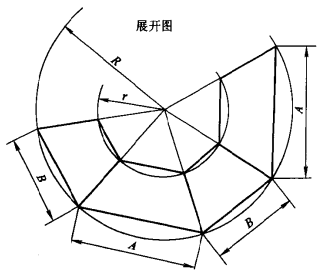圖4（b）
式中 a——矩形台頂口長邊；
b——頂口短邊。
矩形敞口台展開計算
圖5所示為矩形敞口台，已知尺寸為A、B、C、D、H及t。
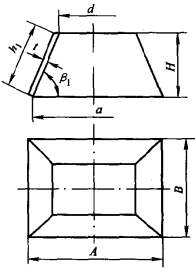圖5（a）
圖5（b）計算式：
史書記載的長方台體積計算
命題 今有芻童，下廣二丈，袤三丈；上廣三丈，袤四丈；高三丈，問：積幾何?
術曰：倍上袤，下袤從之；亦倍下袤，上袤從之；各以其廣乘之；並，以高若深乘之，皆六而一。
答曰：二萬六千五百尺。
(《九章算木.商功》第19題)
芻童，中算立體麥用名司，指長方台。
圖6中上底長()，寬()；下底長()，寬()；高(h)為已給，它的體枳公式是
V芻童=
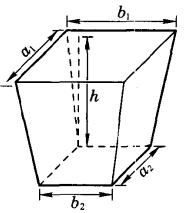圖6證明 為術又可令上下廣袤差相乘，以高乘之，三而一，亦四陽馬。上下廣袤互相乘，並而半之，以高乘之，即四面六塹堵與二立方，並之為芻童積，又可令上下廣袤互相乘而半之，上下廣袤又各自乘，並，以高乘之，三而一，即得也。
(劉徽注芻童術)
