所謂擬凹函式，就是相對坐標橫軸，圖像里沒有下凸現象的曲線。亦即對任意兩點x、y屬於定義域，f(ax+(1-a)y)>=min[f(x), f(y)]。容易證明，若函式是擬凹的，若且唯若其定義域的所有上輪廓集(upper contour set)都是凸的。對於效用函式來說，偏好是凸的，若且唯若效用函式是擬凹的。
基本介紹
- 中文名：擬凹函式
- 外文名：quasiconcave function
- 學科：數學
- 相對：坐標橫軸
- 性質：函式
定義及分類,意義,
定義及分類
擬凹函式：
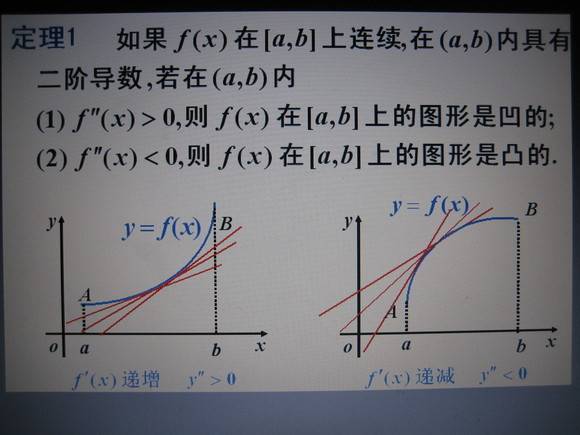
相對坐標橫軸，圖像里沒有下凸現象的曲線。亦即對任意兩點x、y屬於定義域，f(ax+(1-a)y)>=min[f(x), f(y)]。容易證明，若函式是擬凹的，若且唯若其定義域的所有上輪廓集(upper contour set)都是凸的。對於效用函式來說，偏好是凸的，若且唯若效用函式是擬凹的。
嚴格擬凹函式
嚴格擬凹函式：f：D→R是嚴格擬凹函式，若且唯若，對於所有的x1，x2∈D，都有 f（tx1+(1-t)x2）>min{f(x1), f(x2)} ，對於所有的t∈(0,1) 。由定義易知，所有單調一元函式能被認為是此類函式。
意義
集合、關係（等價、傳遞等）、全序、前序、凸凹、擬凸（凹）。了解度量空間的部分知識。了解擬凹函式、凹函式和微分學知識，部分線性代數知識。這些知識將很好地幫助您了解高級個體經濟學的內容，尤其是效用存在性定理的證明、對一般均衡的理解等等。如果要研究經濟個體最優行為這些知識就顯得尤為必要。
至於他的意義，其實就是討論為什麼偏好一定要假定為凸的，偏好的凸性往往被解釋為偏好是邊際替代率是遞減的（注意：是邊際替代率遞減，而非邊際效用遞減！）。從直覺上解釋這種現象，就好比一個人，買蘋果和桔子，他覺得1個蘋果三個桔子比一個桔子三個蘋果好，那么這兩種消費結構直線上的點兩個蘋果兩個桔子，也必定比一個桔子三個蘋果好。這是一個二維的情況。一維則更清楚了，三個蘋果如果比一個蘋果好，那么兩個蘋果一定也比一個蘋果好。隨著維數增加，這個規律也是比較合理的。
另外，最佳化問題中把偏好假設為是凸的，再加上局部非飽和性質，使得對於任意的預算約束下，總有最大效用消費的解。否則，談最佳化是沒有任何意義的。
