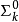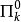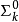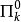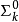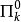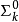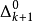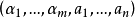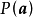基本介紹
- 中文名：描述集合論
- 外文名：descriptive set theory
- 別名：譜系理論
- 屬性：集合論的一種形式和方法
- 相關人物：貝爾，勒貝格，克林等
基本介紹,相關概念,
基本介紹
描述集合論(descriptive set theory)是集合論的一個分支，是研究可以用簡單的方式予以描述的實數集合或其他具有類似結構的集合的數學分支。
有不少數學問題，看來對於任意實數集合是不可回答的，如已經證明，連續統假設在ZFC系統中是不可確定的。還有些數學問題，對任意實數集合而言，其答案令人感到不很協調，例如在選擇公理之下，存在實數的勒貝格不可測集。當人們轉而討論一類特殊的實數集合——有簡單拓撲結構的集合，或以某些簡單方式逐層定義的集合，這些問題就有了明確的、令人感覺協調的答案了。最早的例子是1883年的康托爾-本迪克松定理：實數的每個閉集至多可數或包含有完全子集。注意到實數的完全子集的基數是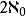
，所以，實數的閉集的基數要么
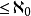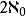，要么=，即連續統假設對閉集成立。19世紀末和20世紀初，波萊爾((F.-É.-J.-)É.Borel)、法國數學家貝爾(R.L.Baire)和法國數學家勒貝格(H.L.Lebesgue)等人創建了描述集合論這一分支，他們以及後來的俄國數學家盧津(Луэин，Н.Н.)、波蘭數學家謝爾品斯基(W.Sierpinski)、俄國數學家蘇斯林(М.Я.Суслин)等人的工作主要是詳細研究波萊爾集合的構造及性質，以及不藉助於諸如選擇公理這種非能行的方法而構造更多類的實數集合，並研究它們的性質，主要研究的是解析集和射影集，它們都有很好的性質，這些研究屬於經典描述集合論。另一方面，藉助於遞歸函式論，美國邏輯學家、數學家克林(S.C.Kleene)和其他邏輯學家從20世紀30年代至20世紀50年代，建立了一套完美的ω子集的可定義性理論。到了1959年，艾迪生(J.W.Addison)證實了克林的可定義性理論和經典的描述集合論實際上討論的是同一對象。今天所討論的描述集合論是結合了這兩種理論的一般理論，即能行描述集合論。現代描述集合論已成為集合論和遞歸論之間的交叉學科，近年來的發展尤為迅猛。
描述集合論又稱譜系理論，是數學的一個分支。波萊爾集(或貝爾函式)的理論和射影集的理論可以認為是譜系理論的一個例子。特別是，我們有這種集合，(或函式)的“級”的概念，並且當級”變得更高時，給出或描述所屬的集合在本質上將變得更加複雜。描述集合論是從所謂法國經驗主義的觀點來研究的一個數學分支。利用遞歸函式的理論，S·C·克林成功地建立了譜系理論，它本質上包含古典描述集合論作為其極端情況。雖然M·截維斯、A·莫斯托夫斯基和其他人基於遞歸函式的理論而研究謂詞的譜系，但是，使該理論成功地發展成幾乎完全的形式的是克林。
相關概念
因為集合或函式都可用謂詞來描述，所以下面的討論將以謂詞為中心，設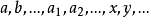
為在自然數集合N上變化的變元，而
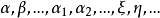為在所有一元數論函式的集合
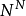上變化的變元，設
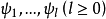為任意給定的數論函式。如果具有兩種類型(自然數和數論函式)變元的謂詞
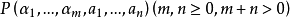能夠從一般遞歸於
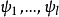的謂詞出發，經過有限次運用邏輯符號：
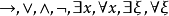而得到，則稱該謂詞是解析(analytic)於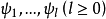的。特別是，當P不用函式量詞
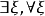而可表示時，則稱它是算術(arithmetical)於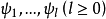的。當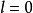
時，謂詞P分別相應地簡稱為解析的和算術的。
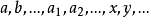
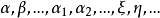
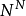
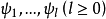
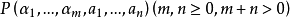
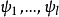
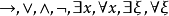
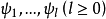
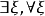
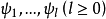
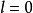
(1)
於是它便可以用寫在下表(a)中的某一形式來表示：
（a）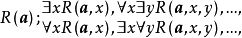
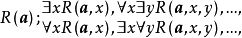
這裡，R為一般遞歸謂詞。我們對(a)中的每一種謂詞形式(或具有這種形式的謂詞全體)，根據它的量詞個數k以及最外邊的量詞為存在量詞或全稱量詞而記為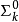
或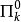
。可用兩種形式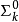和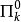來表示的謂詞(或這種謂詞全體)則記為
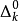。一個謂詞屬於
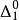的充分必要條件為它是一般遞歸的(類似於Souslin定理)。
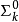
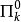
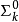
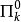
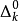
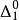
對於k≥1，恆存在一個枚舉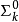(或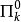)的謂詞全體的枚舉謂詞(enumerating predicate)。例如，對於
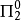和m=n=1而言，存在一個原始遞歸謂詞
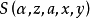，使得當任意給定一個一般遞歸謂詞
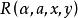時，我們恆有一個自然數
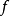，使得
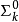
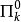
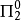
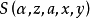
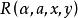
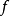
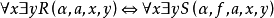
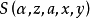
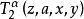
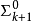
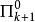
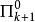
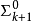
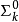
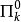
所以，上面的表(a)便是算術謂詞的譜系分類．這個譜系稱為算術譜系(arithmeticalhierarchy)。對每個k≥1，都有一個關於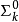(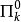)的完備(complete)謂詞，即存在一個僅具有一個變元的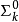(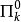)謂詞，使得任何的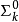(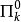)謂詞都可通過將它的一個變元代以一個適當的一般遞歸函式(或更嚴格地，代以一個原始遞歸函式)來表示(完備形式定理(theorem on complete form)。當m=0時，一般遞歸於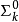的謂詞全體和
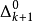是相同的(Post定理)。
