在控制系統最佳化問題中，為了確定控制器的結構及其參數，人們提出了兩類最佳化問題：函式最佳化問題和參數最佳化問題，其中在數學上，解決參數最佳化問題的途徑一般有兩條：間接尋優和直接尋優。由於在控制系統的參數最佳化問題中，一般很難將目標函式Q(a)寫成解析形式，只能在對系統進行仿真的過程中將其計算出來，並且求導Q(a)的過程也不容易實現，基於這些原因，間接尋優法的套用很少。此外，評價最佳化方法好壞的三個要素包括：收斂性、收斂速度、每步疊代所需要的計算量。
基本介紹
- 中文名：控制系統最佳化
- 外文名：Control system optimization
- 最佳化問題：函式最佳化、參數最佳化
- 參數最佳化途徑：間接尋優、直接尋優
- 計算手段：計算機的仿真技術
- 套用領域：飛行控制系統、發電企業等
最佳化問題的專有名詞,尋優參數,約束條件,目標函式,約束最佳化問題的無約束處理,控制系統的最佳化問題,函式最佳化問題,參數最佳化問題,尋優途徑,間接尋優,直接尋優,最佳化方法的評價,收斂性,收斂速度,每步疊代所需要的計算量,控制系統最佳化設計中目標函式的構成,加權性能指標型,誤差積分型,
最佳化問題的專有名詞
尋優參數
假設a為m維尋優參數向量，由於具體取值有待於選擇，因此將其稱為設計變數（或設計參數）。m為設計變數的個數。顯然，當a取不同值，就能夠得到不同的設計方案。因此，需要在m維參數空間中進行最佳化。
約束條件
在最佳化過程中，尋優參數的某些組合情況可能會產生一些明顯不合理的設計。如設計的結果不滿足工程技術要求，或超出了某些允許範圍。而這些允許範圍在數學上是可以化為約束條件的。值得注意的是，在許多工程問題中，約束條件往往不能寫成最佳化參數的顯函式形式，只要是“可計算”的函式即可。
目標函式
在控制器的所有可行設計中，一些較好的設計肯定具有更好的某種（或某些）性質。如果這種性質可以表示為尋優參數的一個可計算的函式，那么只需要尋求這個函式的極值，即可得到“最優”的設計，而這個用來使設計得以最佳化的函式就稱為目標函式。為了強調它對尋優參數的依賴性，可以將其寫成Q(a)。同樣在工程問題巾，Q(a)不一定能寫成顯函式形式，只要求是“可計算”的函式。整個最佳化設計中，選擇目標函式是最重要的決策。如果選擇不當，尋優結果對實際套用可能沒有太大的幫助。
約束最佳化問題的無約束處理
在實際的丁程套用中，尋優參數的取值範圍總是要受到限制的，即總是要在一定的約束條件下來求目標函式的最優解。當這些約束對於尋優參數的限制是很寬的，以至於可以確信在附近約束條件都能夠得到滿足，則可以把它看成無約束最佳化問題來處理。如果在附近約束條件可能被破壞，那么就需要根據約束的不同情況，將約束最佳化問題轉換成無約束最佳化問題來處理。
控制系統的最佳化問題
在實際套用中，為了獲得最佳的設計效果，對於一些複雜的系統，其最佳化過程往往需要採用仿真來完成。隨著計算機的發展為仿真技術提供了更有效的計算手段，使得這種技術得以廣泛地套用。目前，為了確定控制器的結構及其參數，人們提出了兩類最佳化問題：函式最佳化問題和參數最佳化問題。
函式最佳化問題
函式最佳化問題也稱為動態最佳化問題。通常在這類問題中，並不能預先得知控制器的結構，往往需要設計出滿足某種最佳化條件的控制器。在數學上，此類問題也被稱為泛函問題，即所謂尋找最優函式的問題。在控制理論中．通常將這類問題歸為最優控制的範疇。
參數最佳化問題
參數最佳化問題也稱為靜態最佳化問題。在這類問題中，控制器的結構和形式往往是已經確定的，但需要調整或尋找控制器的參數，使系統性能在某種指標意義下達到最優。
尋優途徑
在數學上，解決參數最佳化問題的途徑一般有兩條：間接尋優和直接尋優。
間接尋優
它是一種按照普通極值存在的充分必要條件進行尋優的方法，也可以看做是一種解析方法。由於在控制系統的參數最佳化問題中，一般很難將目標函式Q(a)寫成解析形式，只能在對系統進行仿真的過程中將其計算出來，並且求導Q(a)的過程也不容易實現，基於這些原因，間接尋優法的套用很少。
直接尋優
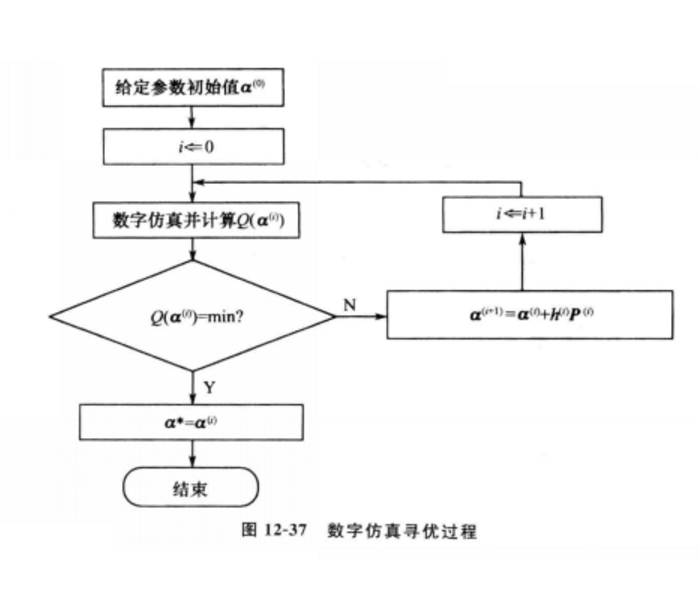
它是一種按照一定的尋優規律改變a，並且直接計算目標函式Q(a)的值，然後判斷Q(a)是否達到極小，當達到極小時，停止搜尋；否則改變a，並計算Q(a)，不斷重複該步驟，直到滿足要求為止。
最佳化方法的評價
在直接尋優法中，不同的確定尋優步距和尋優方向，對應了不同的尋優方法。評價一種最佳化方法的優劣，主要考慮以下幾個方面：
收斂性
尋優過程就是逐步搜尋滿足Q(a)為極小值時的a值，疊代過程的收斂性好壞，表示某種最佳化方法適應範圍的大小。
收斂速度
為了求出同樣精度的極小值點，不同的最佳化方法所需要的疊代次數不同。
每步疊代所需要的計算量
在控制系統的參數最佳化設計過程中，往往需要對a的值進行許多次疊代計算才能搜尋到極小值點，而每次疊代都需要重新計算尋優步長和尋優方向，還需要對系統的運動方程進行仿真並計算目標函式。每步疊代所需的計算量也是決定尋優速度的另一個重要因素。
控制系統最佳化設計中目標函式的構成
加權性能指標型目標函式和誤差積分型目標函式是控制系統最佳化設計中兩大類常用目標函式。
加權性能指標型
加權性能指標型目標函式是一類根據經典控制理論設計系統的性能指標建立起來的，如系統在階躍信號作用下的上升時間，調整時間，超調量及振盪次數N等。通常，對於這些性能指標的要求往往存在矛盾性，此時可以採用加權的方法建立目標函式。
誤差積分型
誤差積分型目標函式是一類由誤差構成的目標函式。對於一般隨動系統，誤差定義為輸出信號和系統輸出之差。一般常用的目標函式如下：
（1）誤差絕對值的積分（IAE）；
（2）誤差平方的積分（ISE）；
（3）時間乘以誤差絕對值積分（ITAE）；
（4）時間乘以誤差平方的積分（ITSE）；
（5）時間平方乘以誤差絕對值的積分（ISTAE）；
（6）時間平方乘以誤差平方的積分（ISTSE）。
