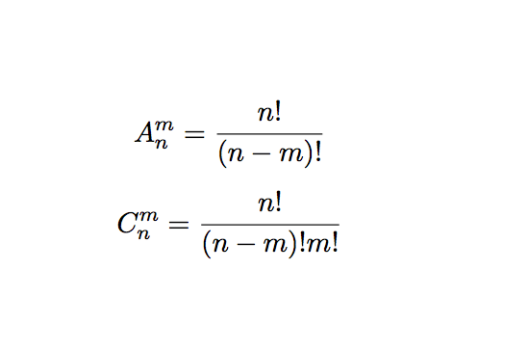排列數公式

排列數

從n個不同的元素中任取m(m≤n)個元素的所有排列的個數，叫做從n個不同的元素中取出m(m≤n)個元素的排列數。記作符號

。A是英文arrangement（排列）的第一個大寫字母。

例如，從7個不同的元素中任取5個元素的排列數為

，從10個不同的元素中任取7個元素的排列數為

。

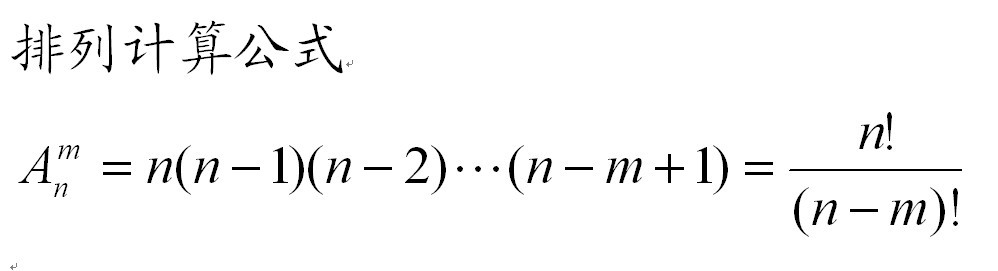
公式A是排列公式，從N個元素取M個進行排列（即排序）。

C：組合數

A：排列數（在舊教材為P）

N：元素的總個數

R：參與選擇的元素個數

!：階乘，如5！=5×4×3×2×1=120

C：Combination 組合

P：Permutation排列 (現在教材為A-Arrangement)

求排列數

可以按依次填m個空位來考慮：假定有排好順序的m個空位,從n個不同元素a₁,a₂,a₃,…,a_n中任意取m個去填空,一個空位填1個元素，每一種填法就對應1個排列，因此，所有不同填法的種數就是排列數。

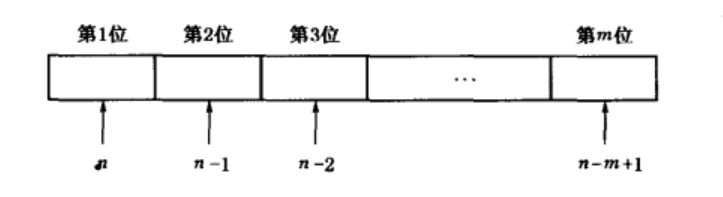
填空可分為m個步驟：

第1步，第1位可以從n個元素中任選一個填上，共有n種填法；

第2步，第2位只能從餘下的n-1個元素中任選一個填上，共有n-1種填法；

第3步，第3位只能從餘下的n-2個元素中任選一個填上，共有n-2種填法；

……

第m步，當前面的m-1個空位都填上後，第m位只能從餘下的n-(m-1)個元素中任選一個填上，共有n-m+1種填法。

根據分步計數原理，全部填滿m個空位共有n(n-1)(n-2)…(n-m+1)種填法。所以得到公式：

這裡n，m∈N^*，並且m≤n這個公式叫做排列數公式其中，公式右邊第一個因數是n，後面的每個因數都比它前面一個因數少1，最後個因數為n-m+1，共有m個因數相乘。

排列與元素的順序有關，組合與順序無關。如231與213是兩個排列，2+3+1的和與2+1+3的和是一個組合

兩個基本原理是排列和組合的基礎

(1)加法原理：做一件事，完成它可以有n類辦法，在第一類辦法中有m₁種不同的方法，在第二類辦法中有m₂種不同的方法，……，在第n類辦法中有m_n種不同的方法，那么完成這件事共有N=m₁+m₂+m₃+…+m_n種不同方法。

(2)乘法原理：做一件事，完成它需要分成n個步驟，做第一步有m₁種不同的方法，做第二步有m₂種不同的方法，……，做第n步有m_n種不同的方法，那么完成這件事共有N=m₁×m₂×m₃×…×m_n種不同的方法。

這裡要注意區分兩個原理，要做一件事，完成它若是有n類辦法，是分類問題，第一類中的方法都是獨立的，因此用加法原理；做一件事，需要分n個步驟，步與步之間是連續的，只有將分成的若干個互相聯繫的步驟，依次相繼完成，這件事才算完成，因此用乘法原理。