指冪不等式是指數函式rx與冪函式xr之間關係的不等式,研究它們之間從實數軸上一個確定的區間後不等式成立。
基本介紹
- 中文名:指冪不等式
- 外文名:Refers to the power inequality
- 套用學科:數學
- 適用領域範圍:數學
定義,證明,性質1,性質2,
定義
假設 r,x和k 是大於1的正[1]實數 ,如果k為閉區間[r/lnr,(r/lnr)2]上的一個正實數時,那么當x>k時,有rx>xr成立。
證明
設f(x)=rx/xr,則lnf(x)=xlnr-rlnx,當x>k時,x>r/lnr>x1/2,
設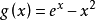 因為
因為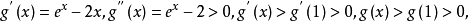 所以
所以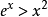 ,兩邊取對數
,兩邊取對數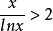 ,所以
,所以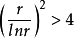
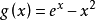
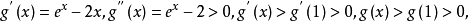
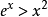
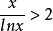
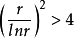
設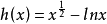 因為x>4,
因為x>4,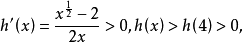
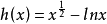
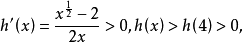
也就是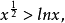 因為
因為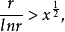 所以
所以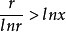 。
。
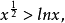
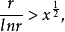
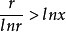
又因為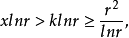 所以
所以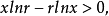 所以
所以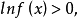
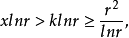
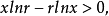
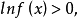
f(x)>1,並且f'(x)/f(x)=lnr-r/x在x>k時,lnr-r/x>0,f'(x)>0,f(x)在x>k上是單調增加的,從而不等式rx>xr成立。
性質1
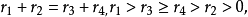
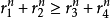
證明:
顯然n=1時,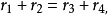
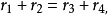
當n=2時,設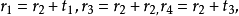 則由已知條件
則由已知條件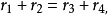 可知
可知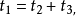 且
且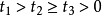
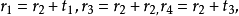
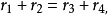
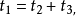
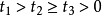
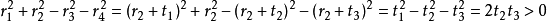
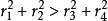
假設當n=k時,
不等式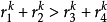 成立
成立
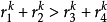
當n=k+1時,
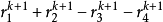
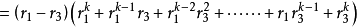
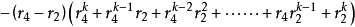
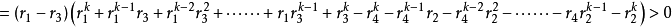
不等式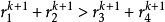
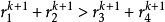
成立。
綜上所述,當
n為自然數,不等式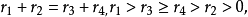
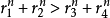 成立
成立
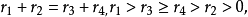
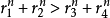
推廣
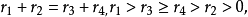
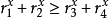
證明:設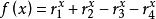
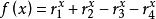
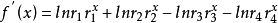
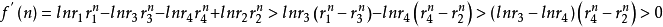
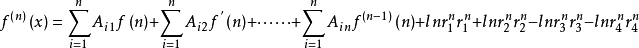
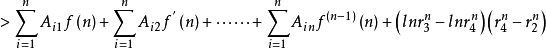
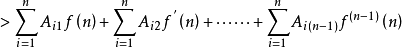
這是個遞推不等式,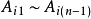 非負,所以
非負,所以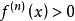 ,根據泰勒公式,
,根據泰勒公式,
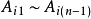
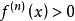
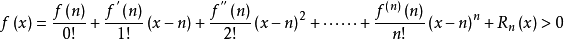
也就是當
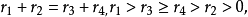
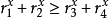
性質2
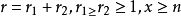
則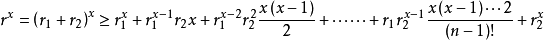
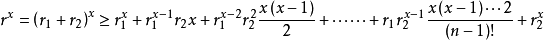
證明:
當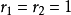 時,
時,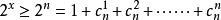 成立
成立
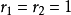
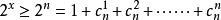
設當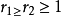 時,
時,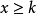 時
時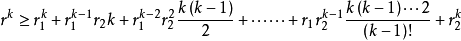
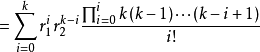 成立
成立
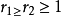
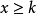
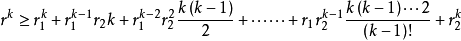
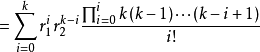
當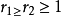 時,
時,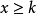 +1 時
+1 時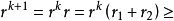
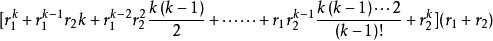
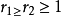
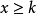
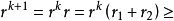
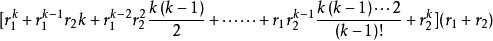
=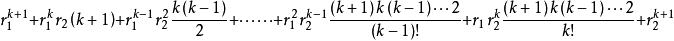
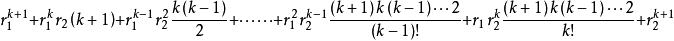
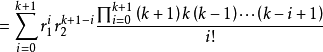
綜上所述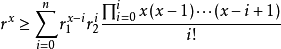 在
在
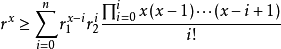
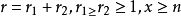
時成立
