拉比諾維奇-法布里康特方程

拉比諾維奇-法布里康特方程(Rabinovich-Fabrikant equations)是 1979年蘇聯物理學家拉比諾維奇和法布里康特提出模擬非平衡介質自激波動的非線性常微分方程組。

基本介紹

• 中文名：拉比諾維奇-法布里康特方程
• 外文名：Rabinovich-Fabrikant equations

簡介

拉比諾維奇-法布里康特方程(Rabinovich-Fabrikant equations)是 1979年蘇聯物理學家拉比諾維奇和法布里康特提出模擬非平衡介質自激波動的非線性常微分方程組：

其中α,γ是控制系統的參數。

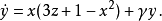
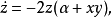
Danca and Chen指出由於拉比諾維奇-法布里康特方程包含平方項，因此比較難以分析，即便選擇的參數相同，但由於求解微分方程組的步驟的不同也會導致不同的吸引子。

數值解

利用Maple中以龍格－庫塔法rkf45為核心的軟體包odeplot和plot、seq可以得出拉比諾維奇-法布里康特方程的數值解的3D動畫圖，以便觀察拉比諾維奇-法布里康特系統隨參數γ和時間t的變化：

參數值：α=1.1，γ=0.803..0.917，t=0...130

初始條件：x(0)=-1,y(0)=0,z(0)=0.5

在t<20時，系統表現為自激振動，當t>20,系統進入混沌態。

平衡點

拉比諾維奇-法布里康特系統具有5個雙曲線平衡點，一個在原點，4個依賴於系統參數α和γ ' ：。

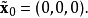
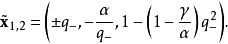
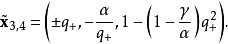
其中：

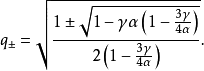
這些平衡點只存在於參數αandγ> 0 的一些區域。

當α=1.1,γ=0.87 代人上式可得：

1. [0,0,0]
   
2. [.46748585798513339859, -2.3530123557983251267, .95430463972208895291]
   
3. [-.46748585798513339859, -2.3530123557983251267, .95430463972208895291]
   
4. [1.3347123182858183570, -.82414763460993508052, .62751354209609286530]
   
5. [-1.3347123182858183570, -.82414763460993508052, .62751354209609286530]
   

γ = 0.87, α = 1.1

當γ= 0.87 andα= 1.1，初始條件為(−1, 0, 0.5).The關聯維數為 2.19 ± 0.01.李雅普諾夫指數,λ約為 0.1981, 0, −0.6581卡普蘭 - 約克量綱,D_KY≈ 2.3010。

γ = 0.1

Danca and Romera指出當參數γ= 0.1、α= 0.98時，系統進入混沌狀態，當α= 0.14時，系統進入極限環。