概念
非線性問題可分為材料非線性問題和幾何非線性問題:一般的有限元法可以用來解決材料非線性問題,但仍囿於小變形的假設,即勿略了因變形造成幾何尺寸的改變所導致應力的微小變化,且略去應變的二次冪,對於幾何大變形問題,雖然原則上可以將荷載分成若干級,在每一級荷載施加後算出結構的應力、應變和新的位置。以此為基礎再計算出結構中各個單元的剛度矩陣,組成總剛度矩陣後再加下一級荷載依次求解。可見,其計算工作量是相當繁複的。
岩土介質是一種為眾多節理裂縫等弱面所切割的地質體。岩土力學的問題往往牽涉到非線性大變形的問題。例如,地下巷道中的底問題,底賺使巷道的斷面縮小,影響走車和通風,需要經常拉底,有時累計拉底的岩石體積可以充滿整個巷道而有餘。象這樣的問題現在通用的有限元法和邊界元法都無能為力,只能求助於拉格朗日元法。拉格朗日元法正是這樣一種分析非線性大變形問題的數值方法,這種方法依然遵循連續介質的假設,利用差分格式,按時步積分求解,隨著構形的變化不斷更新坐標,允許介質有大的變形。
拉格朗日元法的名字淵源於
流體力學中跟蹤質團運動的一種方法,實際上是連續介質力學中對運動的物質描述方法,在非線性連續體力學中叫拖帶坐標系或嵌含坐標系方法。
拉格朗日元法的格線劃分
拉格朗日元法用差分方法求解,因此首先要分成格線,物理格線(圖1)影射在數學格線(圖2)上,這樣數學格線上的某個編號為
,
的結點就與物理格線上相應結點的坐標
,
相對應。也可以將數學格線想像為一張橡皮做的網,拉扯以後可以變為物理格線的形狀。
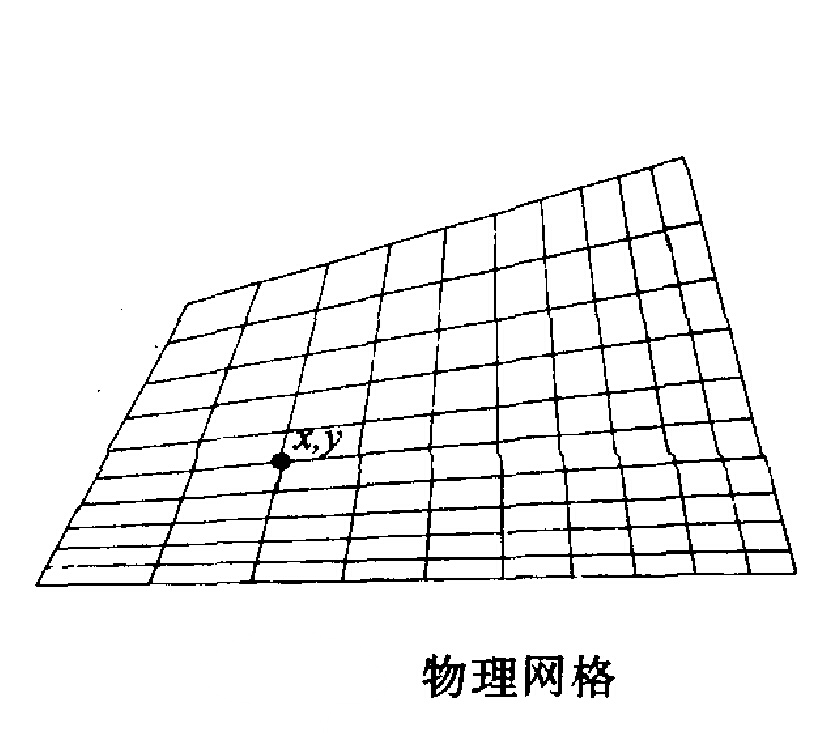 圖1
圖1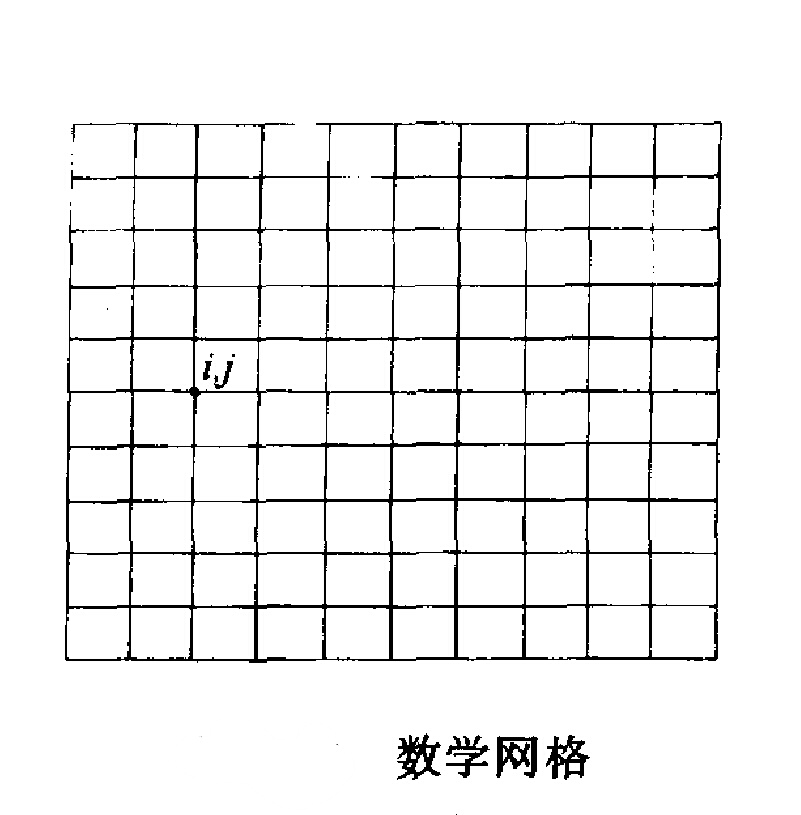 圖2
圖2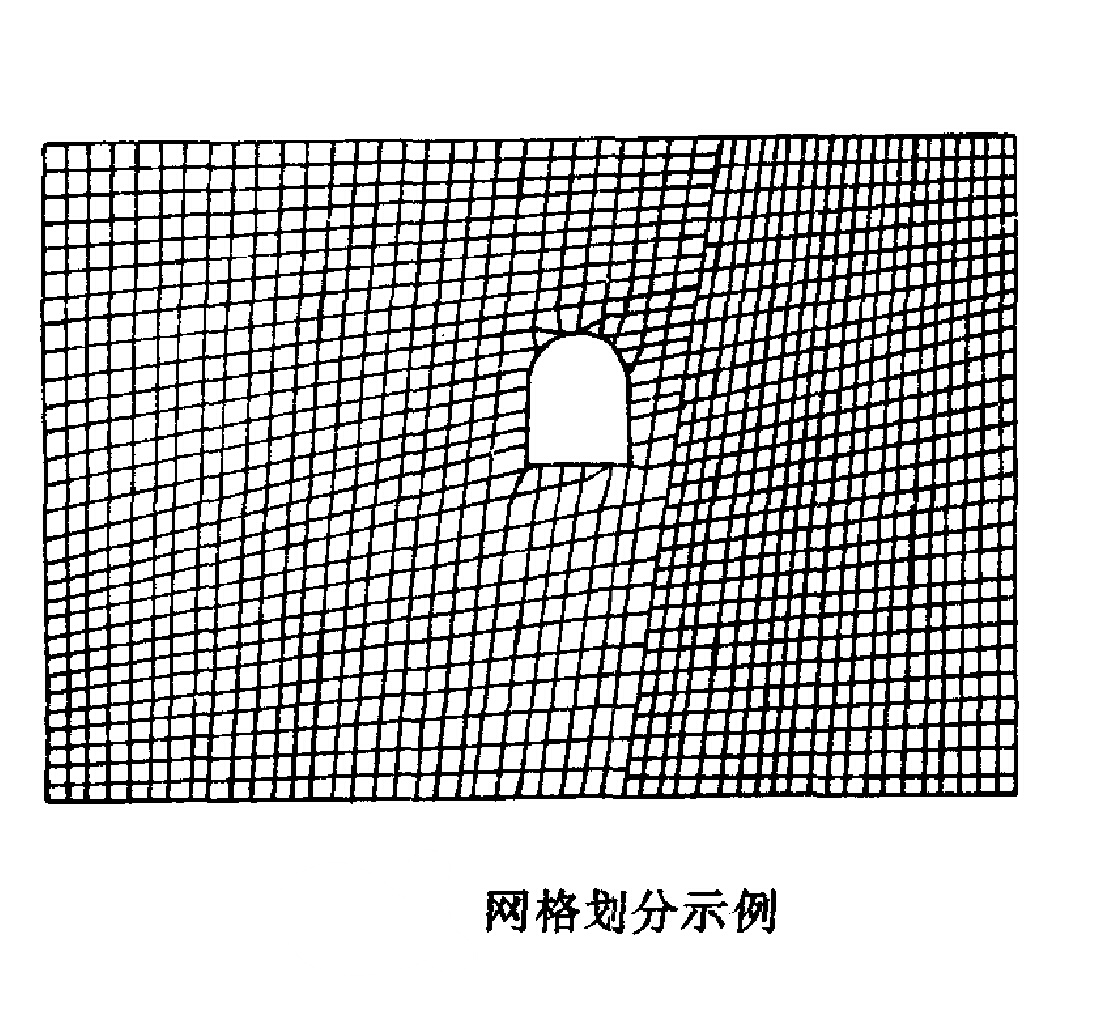 圖3
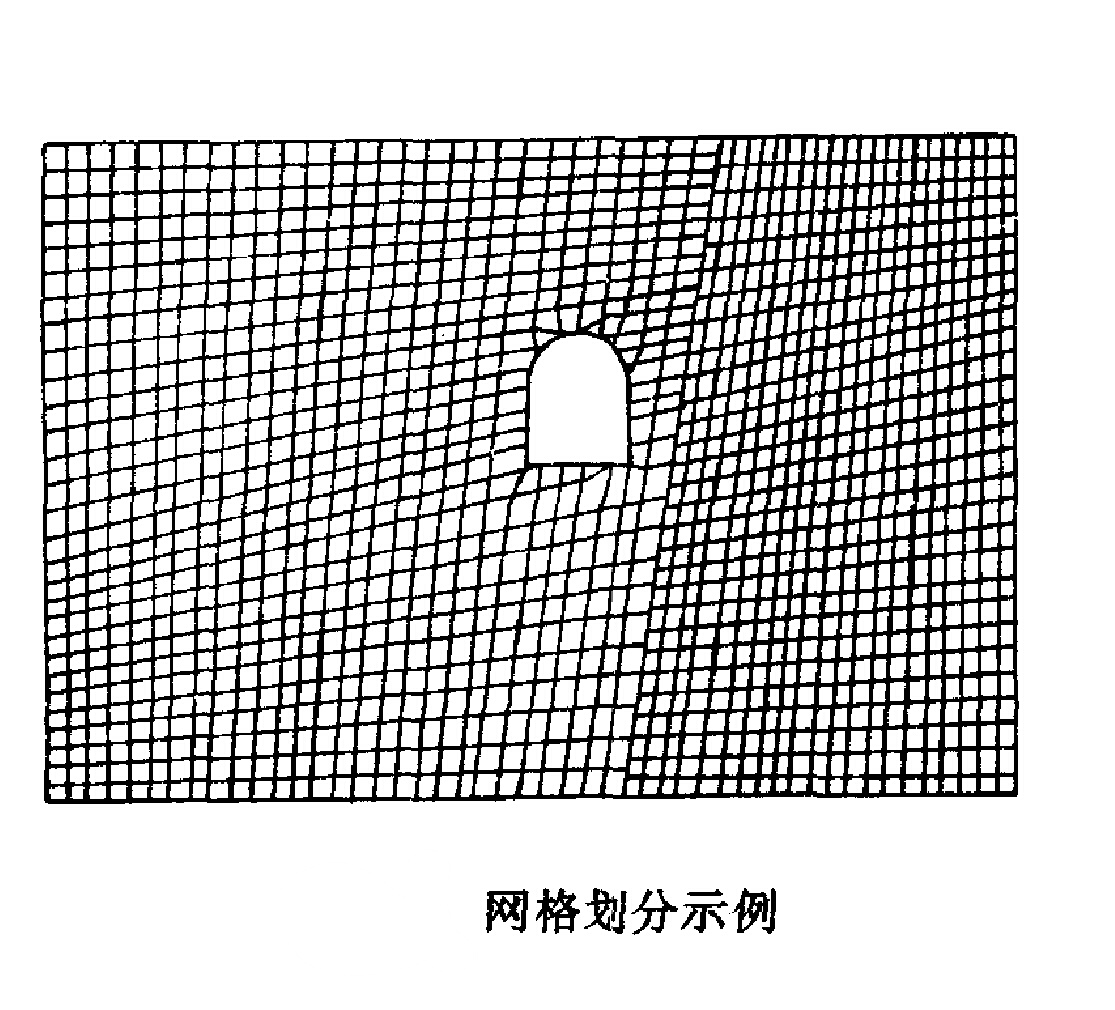
圖3分成的格線只要有序也可以具有不規則的形狀,圖3所示為在斷層一側的巷道周圍格線劃分的示例。格線基本上是四邊形的,但在邊界等不規則的地方也可以用三角形格線來擬合。
基本原理
先舉一個一維桿的例子。假定桿為彈性,側面不受限制,兩端受拉,桿的密度為
,彈性模量為
,其本構關係為
,桿的運動平衡方程為
。
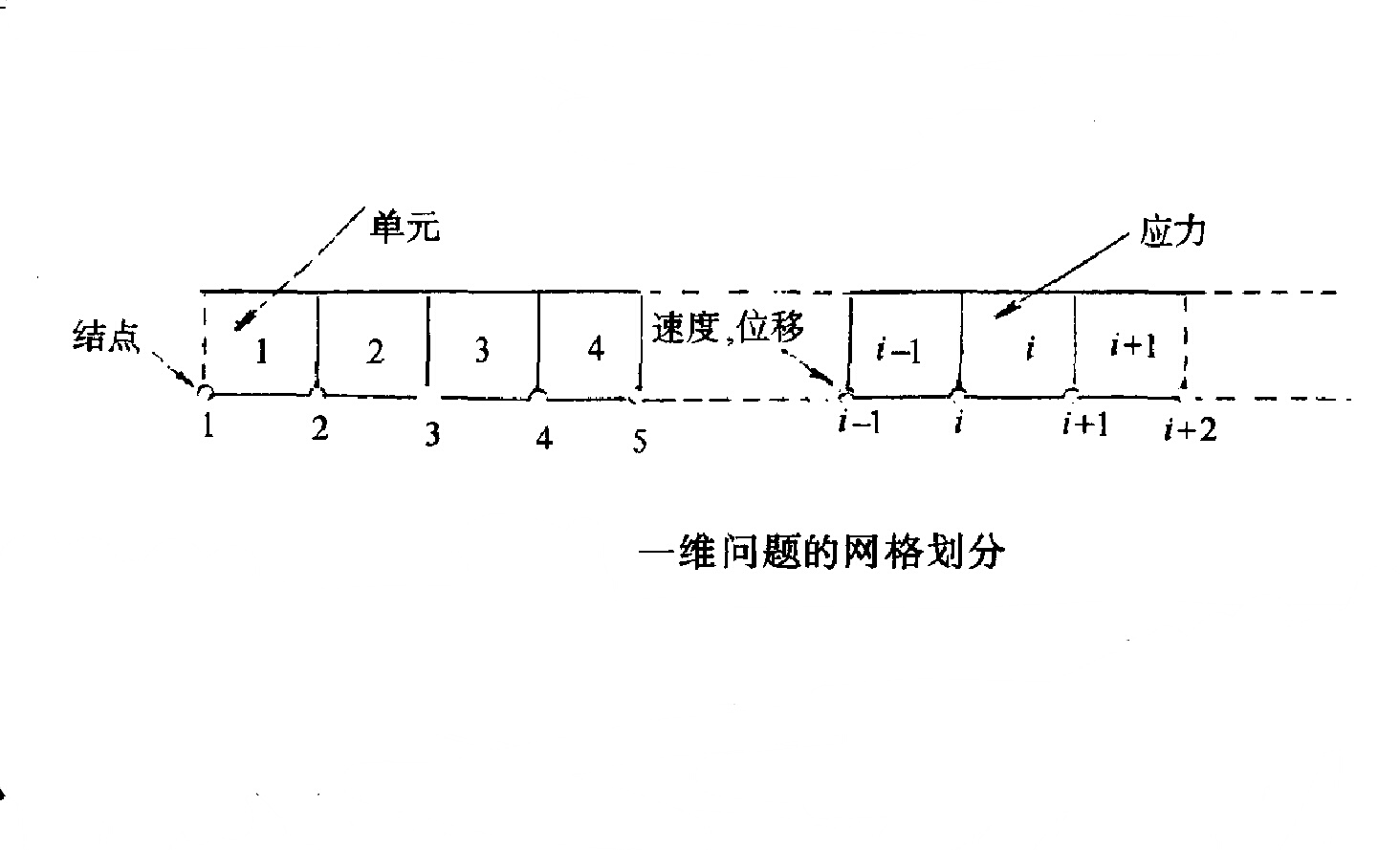 圖4
圖4一維問題的格線劃分如圖4所示,結點順序編號,結點之間區域(或可稱格線、單元)的編號從其左側的結點開始編號。我們約定,凡張量(例如應力)和純量(例如密度)定義在格線中,凡矢量(例如速度)定義在結點上。
差分方程就其求解的數值方法而言可以分為兩大類:一類是隱式方法,另一類是顯式方法。隱式方法要解一個線性聯立方程組,所有的未知數一次求解,隱式方法需要存儲一個大的矩陣,對於非線性問題還要多次分段線性化後用增量法求解。顯式法則不用解方程組,因為等式右邊的值均為已知,可將右邊的表達式求值後賦值給左邊的未知數就可以了,這個過程也就是同時更新所有的變數。某一時步時的所有“老”的變數為其後一時步的“新”的變數所代替,而時間則又前進了一步。所以,顯式法可以隨著時間的推移跟蹤運動的發展。顯式法的缺點是時步的大小要選擇恰當,過大了會使解不穩定,過小則疊代次數太多,需要的機時長。拉格朗日元法系採用顯式解法。
時步選擇的原則是要使計算的速度大於縱波傳播的速度,也就是從物理上講,在一個時步之內,“信息”不能由一個單元傳到另一個單元。

 圖1
圖1 圖2
圖2 圖3
圖3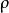
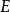
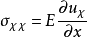
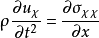
 圖4
圖4