投射極限是範疇論的一個概念。
基本介紹
- 中文名:投射極限
- 外文名:projective limit
inverse limit
limit - 所屬學科:範疇論
- 別名:反極限、極限
定義
圖表
極限
投射極限是範疇論的一個概念。

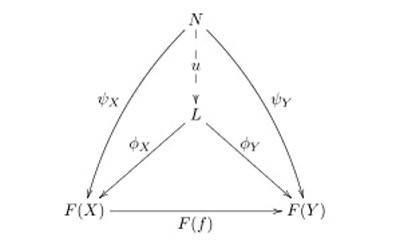
投射極限是範疇論的一個概念。定義設C與J為範疇,Δ:C→CJ為對角函子,F:J→C為CJ中的對象。則從Δ到F的泛態射<LimF,v:ΔLimF→F>稱為F的投射極限。其中LimF稱為極限對象,v稱為極限錐。圖...
極限錐是範疇論中的一個概念。定義 設C與J為範疇,Δ:C→C為對角函子,c為C的對象,函子F:J→C為C的對象。若F的歸納極限為,則μ稱為從基F到頂點c的極限錐;若F的投射極限為,則ν稱為從頂點c到基F的極限錐。性質 若對...
投射f模(projective f-module)具有格序結構的投射模.投射f模,具有格序結構的投射模.設P是有單位元的左f環上的左f模。若給定f模M,N,滿L同態}: M->N和L同態}p: P->N,存在L同態尹:P->M,使得尹}=}P,即是可換的,...
射電望遠鏡(英文名稱radio telescope)與反射式光學望遠鏡相似,投射來的電磁波被一精確鏡面反射後匯交於一個公共焦點。與光學望遠鏡不同的就是光學望遠鏡是對可見光聚焦成像,而射電望遠鏡則是對長波電磁波進行匯聚。射電望遠鏡是指觀測和...
《極限籃球世界》是一部競技類型網路小說,作者是二次方的天空。內容簡介 極限世界,球技稱霸,強者為尊!易赫自地球穿越,自帶極限籃球系統!“極限變速!”“極限跳躍!”“極限投射!”“淡定,我不過只是籃球場上的神,而已。”S級的...
目次:範疇,乘積,投射極限和歸納極限;同調代數基本概念;層;層的上同調;緊黎曼曲面和阿貝爾簇。作者簡介 本書是德國著名數學家,其代表作Lectures on Algebraic Geomedtry I and II是數學領域廣泛採用的經典教材。
函子H:I→C有極限(或余極限)若且唯若函子FH:I→D有投射極限(或歸納極限)Fl。這可以用於等化子、積與余積,等等。套用於核與余核,我們發現等價F是一個正合函子。C是一個笛卡兒閉範疇(或一個拓撲斯)若且唯若D是笛卡兒...
5.3.2武器投射的極限偏差 5.3.3 武器投射偏差機率分布的均方差和圓機率偏差 5.4直升機機載武器射擊精度 5.4.1 直升機機載空地制導武器的射擊精度 5.4.2直升機機載非制導武器的射擊偏差 5.5機載武器的命中機率 5.5.1 單發...
浩瀚星空的主宰者,能在星界投射力量到物質世界形成化身,化身的力量能級相當於真正傳奇六階,因卓越的境界和力量掌控擁有頂尖七階的戰力。因為星界特性會根據自身所能承載的能量消耗決定了自身的存在時間以及消耗強度,一旦超過消耗界限會被歸...
另納米陶瓷光學反光器有98%的熱反射率,能將熱能往光照射區投射,避免燈座內的電子裝置長時間處於高溫而導致壽命減短的問題,除了節能,納米陶瓷光學反光器有效的延長了燈具的使用壽命!簡介 名稱:納米陶瓷光學反光器,簡稱納米反光器或者...
試驗設定了複雜的極限條件,這種新型魚雷由潛艇發射,它沒有被軍艦投射的誘餌所欺騙,而是繞過它們,一聲怒吼,將數千噸的靶船迅速沉沒。這標誌著我國新型大深度高速智慧型魚雷定型試驗畫上圓滿句號,將列裝潛艇部隊。相對於形形色色的亞音速...
