戈登股利增長模型

戈登股利增長模型又稱為“股利貼息不變增長模型”、“戈登模型(Gordon Model)”，在大多數理財學和投資學方面的教材中，戈登模型是一個被廣泛接受和運用的股票估價模型。

基本介紹

• 中文名：戈登股利增長模型
• 別稱：股利貼息不變增長模型
• 推廣者：麥倫·戈登
• 涉及：股票價格和股息固定增長率等

定義

該模型通過計算公司預期未來支付給股東的股利現值，來確定股票的內在價值，它相當於未來股利的永續流入。戈登股利增長模型是股息貼現模型的第二種特殊形式，分兩種情況：一是不變的增長率；另一個是不變的增長值。

不變增長模型有三個假定條件：

1、股息的支付在時間上是永久性的。

2、股息的增長速度是一個常數。

3、模型中的貼現率大於股息增長率。

在戈登模型中，需要預測的是下一期股利及其年增長率，而不是預計每一期的股利，以下就是固定股利增長率政策下未來股利的流入量表：

	第1期	第2期	第3期	...
股利	D1	D1(1 + g)1	D1(1 + g)2	...
00	01	02	03	...
V				...

將所有現金流折現到0點

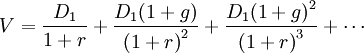
套用等比數列的求和公式，上式可以簡化為：

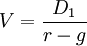
由於這個公式十分簡單，因此人們很容易忘記這是一個無限項的運算。

根據這個模型，公司的股利政策會對股票價值產生影響。這個模型十分有用，原因之一就是它使投資者可以確定一個不受當前股市狀況影響的公司的絕對價值或“內在價值”。其次，戈登模型對未來的股利（而不是盈餘）進行計量，關注投資者預期可以獲得的實際現金流量，有助於不同行業的企業之間進行比較。儘管這個模型的概念十分簡單，但是除了一些機構投資者以外，套用範圍並不廣泛，因為如果缺乏必要的數據和分析工具，它用起來就非常麻煩。

股利增長模型被麥倫·戈登教授得以推廣，因此被稱為“戈登模型”，這個模型幾乎在每一本投資學教材中都會出現。紐約大學教授Aswath Damodaran在他所著的《投資估價》一書中寫道：“從長期來看，用戈登模型低估（高估）的股票勝過（不如）風險調整的市場指數。”儘管任何一種投資模型都不可能永遠適用於所有股票，但戈登模型仍被證明是一種可靠的方法，用以選擇那些在長期從總體上看走勢較好的股票。它應該是投資者用來在其投資組合中選擇其中一些股票時運用的有效工具之一。

主要內容

該模型認為，用投資者的必要收益率折現股票的必要現金紅利，可以計算出股票的理論價格。

戈登模型(Golden Model)揭示了股票價格、預期基期股息、貼現率和股息固定增長率之間的關係，用公式表示為：

其中：P為股票價格；D為預期基期每股股息；i為貼現率；g為股息年增長率。

由於股票市場的投資風險一般大於貨幣市場，投資於股票市場的資金勢必要求得到一定的風險報酬，使股票市場收益率高於貨幣市場，形成一種收益與風險相對應的較為穩定的比價結構，所以戈登模型中的貼現率i應包括兩部分，其一是貨幣市場利率r，其二是股票的風險報酬率i′，即i=r+i′，故戈登模型可進一步改寫為如下公式：

這一模型說明股票價格P與貨幣市場利率r成反向關係，r越高，股價P越低，反之亦然，這一關係被現今各國實踐所證實。

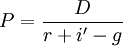
戈登股利增長模型的公式詳解：

貼現現金流模型的公式如下：

式中：

如果我們假設股利永遠按不變的增長率增長，那么就會建立不變增長模型。T時點的股利為：

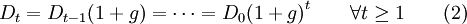
將(2)式代入(1)式，得到：

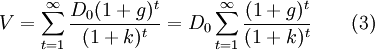
運用數學中無窮級數的性質，如果k > g ，可知：

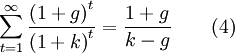
把公式(4)代入公式(3)中，得出不變增長模型的價值公式：

假如去年某公司支付每股股利為1.80元，預計在未來日子裡該公司股票的股利按每年5%的速率增長。因此，預期下一年股利等於1.80×(1+0.05)=1.89(元)。假定必要收益率是11%，根據公式(5)可知，該公司的股票等於1.80×(1+0.05)/(0.11-0.05)=1.89/(0.11-0.05)=31.50(元)。而當今每股股票價格是40元，因此股票被高估8.50元，建議當前持有該股票的投資者出售其股票。

方程(5)可用於解出不變增長證券的內部收益率。首先，用股票的當今價格代替V，其次，用k * 代替k，其結果是：

經過變換，可得：

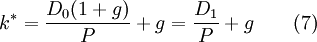
用上述公式來計算上例公司股票的內部收益率，得出：

由於該公司股票的內在收益率小於其必要收益率，顯示出該公司股票價格被高估。

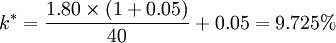
關係

零增長模型實際上是不變增長模型的一個特例。假定增長率g等於0，股利將永遠按固定數量支付，這時，不變增長模型就是零增長模型。

從這兩種模型來看，雖然不變增長的假設比零增長的假設有較小的套用限制，但是在許多情況下仍然被認為是不現實的。由於不變增長模型是多元增長模型的基礎，因此這種模型極為重要。