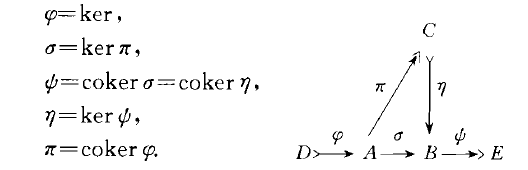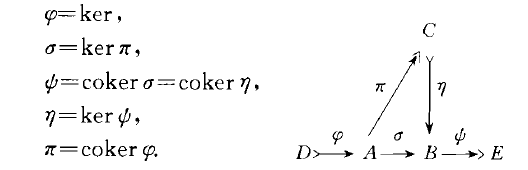態射像(image of a morphism)群論中同態像概念在阿貝爾範疇中的推廣.由阿貝爾範疇的定義可知:加性範疇留為阿貝爾範疇的充分必要條件是對任一態射aEHom(A,B),都有如下的可換圖,其中,表滿態射,表單態射,對阿貝爾範疇留,這裡的(C,帕稱為a的像,記為Im a = (C,帕,有時也稱甲為a的像,記為Ima=r}.若留為群範疇,在同構意義下,C就是群同態a的像,也就是說,(C,帕為a的像.可對偶地定義態射的上像.對一般的範疇留可如下定義留中態射.f : X->Y的像:若有Y的子對象Y'與單態射g:Y'->Y,,使有態射二:X ->Y'滿足f-g},且對Y任意的子對象Y,與單態射g} : Yi-'Y,使有態射二} : X->Y,滿足f=g,},,則必有態射h:y}->Y使gih = g.此時稱(Y',g)為態射.f:X}Y的像.值得注意的是,這樣定義的像未必存在.若在一個範疇中,每一個態射都有(按此定義的)像,則稱此範疇為帶像範疇.阿貝爾範疇是帶像範疇,此時本條目中兩種定義是一致的.