愛可爾斯定理

愛可爾斯定理(Echols theorem)是歐幾里得幾何的兩個著名定理，是關於兩個以及三個正三角形有關性質的定理，愛可爾斯(Echols)於1932年發表了這些定理及其證明，證明採用複數的證法。定理1.若△Z₁Z₂Z₃和△U₁U₂U₃都是同向正三角形，則線段Z₁U₁，Z₂U₂，Z₃U₃的中點作成正三角形；定理2.若△Z₁Z₂Z₃，△U₁U₂U₃，△V₁V₂V₃都是同向正三角形，則△Z₁U₁V₁，△Z₂U₂V₂，△Z₂U₂V₂的重心作成正三角形。該定理是愛可爾斯(Echols)在1932年論述的，這兩個定理故名愛可爾斯定理。

基本介紹

• 中文名：愛可爾斯定理
• 外文名：Echols theorem
• 所屬學科：數學（平面幾何）
• 簡介：關於兩個以及三個正三角形性質
• 提出者：愛可爾斯(Echols)

定理及簡史

愛可爾斯定理1

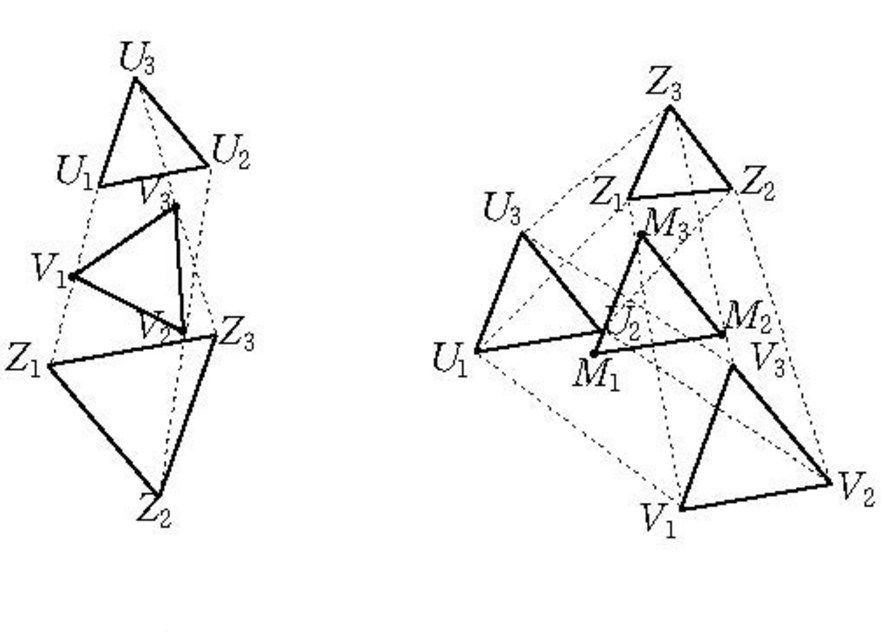
若△A₁B₁C₁和△A₂B₂C₂都是正三角形，則線段A₁A₂、B₁B₂、C₁C₂的中點也構成正三角形。

愛可爾斯定理2

若△A₁B₁C₁、△A₂B₂C₂、△A₃B₃C₃都是正三角形，則△A₁A₂A₃、△B₁B₂B₃、△C₁C₂C₃的重心也構成正三角形。

這是愛可爾斯(Echols)1932年在美國《數學月刊》上論述過的問題(愛可爾斯定理1曾被蕪湖市選用作為1983年中學生數學競賽試題)。

定理的證明

首先我們證明愛可爾斯定理1，這個定理有多種證法，下面的證明是比較簡捷的。

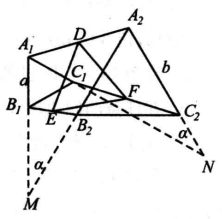
圖1

證明 如圖1，設正△A₁B₁C₁的邊長為a，正△A₂B₂C₂的邊長為b，A₁A₂、B₁B₂、C₁C₂的中點分別為D、E、F，延長A₁B₁、A₂B₂交於M，A₁C₁、A₂C₂交於N，因為∠MA₁N=∠MA₂N = 60°，所以A₁、M、N、A₂四點共圓，所以∠M=∠N(設為α，0°≤α<180°)。在四邊形A₁B₁B₂A₂和四邊形A₁C₁C₂A₂中，由相關定理得到的公式(Ⅱ)

得DE= DF，同理可得DE=EF，故△DEF為正三角形，下面證明愛可爾斯定理2。

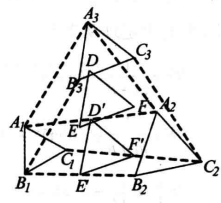
圖2

證明 設A₁A₂、B₁B₂、C₁C₂的中點分別為D'、E'、F'(圖2)，則由愛可爾斯定理1知△D'E'F’為正三角形，又設D、E、F分別為A₃D'、B₃E'、C₃F'上的點，且 ，則D、E、F分

別為△A₁A₂A₃、△B₁B₂B₃、△C₁C₂C₃的重心，由相關定理的公式( * ):

中，令 ，可得DE = DF=EF，即△DEF為正三角形。

定理的推廣

愛可爾斯定理1的推廣

將中點D、E、F推廣，可得

定理1 設△A₁B₁C₁、△A₂B₂C₂均為正三角形，D、E、F分別為A₁A₂、B₁B₂、C₁C₂上的點，且

則△DEF為正三角形。

如將正三角形向相似三角形推廣，則有

定理2 設△A₁B₁C₁、△A₂B₂C₂同向相似，D、E、F分別為A₁A₂、B₁B₂、C₁C₂上的點，且

則△DEF也與△A₁B₁C₁及△A₂B₂C₂同向相似。

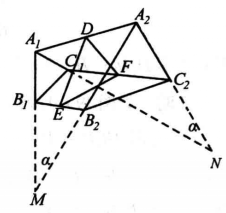
圖3

將三角形向多邊形推廣，可得

定理3 設n邊形 與n邊形 同向相似，點 分別在 上，且

則n邊形 與n邊形 及n邊形 同向相似。

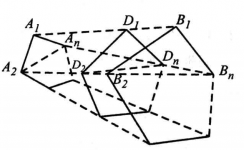
圖4

愛可爾斯定理2的推廣

定理4 (如圖5)設△A₁B₁C₁、△A₂B₂C₂、△A₃B₃C₃均為正三角形，D'、E'、F'分別為A₁A₂、B₁B₂、C₁C₂上的點，且

D、E、F分別為 上的點，且

則△DEF為正三角形。

證明 由於△A₁B₁C₁、△A₂B₂C₂均為正三角形，由已知及定理1得△D'E'F’為正三角形。

同理，對△A₃B₃C₃和△D'E'F'套用定理1得△DEF為正三角形。

定理5 △A₁B₁C₁、△A₂B₂C₂、△A₃B₃C₃同向相似，D'、E'、F'分別為A₁A₂、B₁B₂、C₁C₂上的點，且

D、E、F分別為 上的點，且

則△DEF與原三個三角形同向相似。

證明 由定理2，△D'E'F'與△A₁B₁C₁、△A₂B₂C₂同向相似；△DEF與△A₃B₃C₃及△D'E'F'同向相似，故△DEF與△A₁B₁C₁、△A₂B₂C₂、△A₃B₃C₃同向相似。

定理6 n邊形 同向相似， 分別為 上的點，且

分別為上的點，且

則n邊形與n邊形同向相似。

定理的套用

例1 如圖5，△ABC、△ADE均為正三角形，F、G、H分別為AB、CD、AE的中點，求證△FGH為正三角形。

證明對正△ABC和正△EAD套用愛可爾斯定理1，即得△FGH為正三角形。

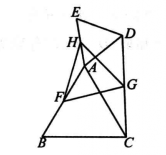
圖5

例2 套用愛可爾斯定理證明拿破崙定理。

證明 如圖6，對正△XCB、正△CYA、正△BZA，套用愛可爾斯定理2，即得△DEF為正三角形。

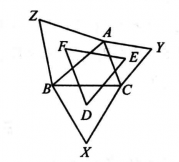
圖6