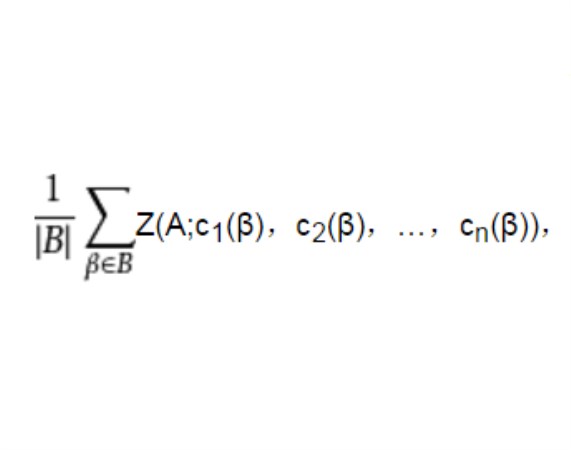德布萊英定理

德布萊英定理(de Bruijn's theorem)是波利亞定理的推廣，哈拉里(F.Harary)推廣了德布萊英定理。

基本介紹

• 中文名：德布萊英定理
• 外文名：de Bruijn's theorem
• 所屬學科：數學（組合學）
• 簡介：波利亞定理的推廣

基本介紹

若兩置換群A和B分別作用於兩有限集X={x₁，x₂，…，x_n}和Y={y₁，y₂，…y_m}，則可定義冪群B^A={(α，β)|α∈A，β∈B}對函式集Y^X={f|f：X→Y}的作用為(α，β)f(x)=β(f(αx))。若有(α，β)f=f′，則稱f，f′是等價的，記為f~f′，~為一等價關係。於是，Y^X被分為若干等價類之並，這些等價類稱為函式式樣或函式軌道，德布萊英定理斷言：函式式樣的個數等於

式中群A的循環指標為

其中β的型為。

德布萊英定理的推廣

哈拉里(F.Harary)推廣了德布萊英定理。

設Y為可數集，Y至少含2元，定義權函式w：Y→R，R⊂N₀，N₀為非負整數集；又定義函式f的權

設k∈R，Y的子集Y_k={y|y∈Y，w(y)=k}，且|Y_k|是有限的，|Y_k|=C_k。若B(Y_i)={β(y)|β∈B，y∈Y_i}，則函式集Y^X被冪群B^A作用所分出的各個式樣中的函式有等權的充分必要條件是B(Y_i)=Y_i，i∈R，若條件B(Y_i)=Y_i，滿足i∈R，則可定義式樣F的權為w(F)=w(f)，其中f∈F，記β=β_i，式中β_i(y)=β(y)，這裡y∈Y_i，若權為k的式樣為C_k個，則式樣依權展開的生成函式為

於是

式中Z(A;s₁，s₂，…，s_n)為A的循環指標，

β_i的型為。