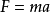微擾理論是從相關問題的確切解中找出問題的近似解的數學方法。該技術的一個關鍵特徵是將問題分解為“可解決”和“擾動”兩部分。如果手頭的問題無法精確地解決，微擾理論是可以採用的，但只是可以通過在問題的數學描述中增加一個“小”項。
微擾理論推導出了在一些“小”參數（稱為微擾序列）中的形式冪級數的期望解的表達式，量化了與問題的偏差。這個系列的主要參數是求出問題的精確解，而由於偏離了初始問題，進一步的參數描述了解的偏差。在形式上，我們有近似於完整解A，一個小參數（這裡稱為ε）的系列。
基本介紹
- 中文名：微擾理論
- 外文名：Perturbation theory
- 學科：數學
- 本質：從確切解中找出問題的近似解
- 作用：量化了與問題的偏差
- 相關名詞：數值分析方法
簡介,舉例,歷史,擾動秩序,在化學,
簡介
微擾理論是從相關問題的確切解中找出問題的近似解的數學方法。該技術的一個關鍵特徵是將問題分解為“可解決”和“擾動”兩部分。如果手頭的問題無法精確地解決，微擾理論是可以採用的，但只是可以通過在問題的數學描述中增加一個“小”項。
微擾理論推導出了在一些“小”參數（稱為微擾序列）中的形式冪級數的期望解的表達式，量化了與問題的偏差。這個系列的主要參數是求出問題的精確解，而由於偏離了初始問題，進一步的參數描述了解的偏差。在形式上，我們有近似於完整解A，一個小參數（這裡稱為ε）的系列，如下所示：
在這個例子中，A0是初始問題的已知解，A1，A2，...代表可以通過一些系統過程疊代地找到的高階項。 對於小ε，該系列中的這些高階項逐漸變小。
通過對序列進行截斷來獲得近似的“擾動解”，通常通過僅保留前兩個項，初始解和“一階”擾動校正。
微擾理論與數值分析中使用的方法密切相關。最早使用現在稱為微擾理論的方法是處理天體力學中其他無法解決的數學問題：例如月球的軌道，其與簡單的克卜勒橢圓運動明顯不同，因為地球的相互作用引力，太陽。
微擾理論方法從原始問題的簡化形式開始，這可以準確地解決。在天體力學中，通常是克卜勒橢圓形。在非相對重力下，當只有兩個引力體（即地球和月球）時，橢圓是正確的，但當有三個或更多個物體（例如地球，月球，太陽和太陽系的其餘部分），並且當使用廣義相對論的配方來描述引力相互作用時不太正確。
但是，簡化的問題被“擾亂”，使得擾動解的實際情況更接近於原始問題中的公式，例如包括第三體（太陽）的引力吸引力。通常，代表現實的“條件”是具體表達一些物理定律的公式（或幾個），如牛頓第二定律，力加速度方程，
在該示例的情況下，基於重力相關體的數量來計算力F；使用微積分從月球軌道上獲得加速度a。 這兩種形式有兩種形式：由簡化引起的力和加速度的近似值，以及力和加速度的假設精確值，這將需要完整的計算結果。
由於適應擾動而導致的輕微變化本身可能已經被簡化了，被用作修正近似解。 由於每一步都引入了簡化，糾正是不完美的，修正後的解滿足的條件與實際要求的方程不完全匹配。 然而，即使只有一個循環的修正通常提供了一個很好的近似答案，應該是真正的解。
沒有必要只在一個循環的修正停止。可以將部分校正的解重新用作另一個擾動和校正周期的新起點。原則上，找到越來越好的更正的周期可能無限期。實際上，通常在一個或兩個修正周期停止。該方法的常見難點在於，糾正逐漸使新解變得更加複雜，因此每個循環比上一個更正循環更難以管理。據報導，牛頓說，關於月球軌道的問題，“是我的頭疼”。
這個一般程式是先進科學和工程中廣泛使用的數學工具：從簡化的問題開始，並逐漸增加校正，使修正後的問題與原始公式更接近地匹配。對於古代文明首先用於計算某些數字（如平方根）的“猜測，檢查和修復”方法的數學函式的自然延伸。
舉例
（1）“數學描述”的例子是：代數方程，微分方程（例如，運動方程或波動方程），自由能（統計力學），輻射傳遞一個哈米爾頓運算元（量子力學）。
（2）可以在擾動中找到的解的例子：等式的解（例如，粒子的軌跡），一些物理量（例如平均磁化強度）的統計平均值，量子力學問題的基態能量。
（3）可以解決問題的例子有：線性方程式，包括線性運動方程（諧波振盪器，線性波動方程），非相互作用粒子的統計學或量子力學系統（或一般來說，僅包含術語的哈密爾頓運算元或自由能所有自由度都是二次方）。
（4）處理的“擾動”的例子：對運動方程，粒子之間的相互作用的非線性貢獻，哈密爾頓/自由能中的較高權力項。
（5）對於涉及粒子間相互作用的物理問題，擾動序列的項可以使用Feynman圖進行顯示（並進行操作）。
歷史
微擾理論首先被設計為解決計算太陽系中行星運動的其他棘手問題。例如，牛頓萬有引力定律解釋了兩個天體之間的引力，但是當第三體被添加時，問題是“每個身體如何拉動每一個”？牛頓方程只允許分析兩個物體的質量。天文觀測的逐漸提高的準確性導致了牛頓引力方程解的準確性的增加需求，導致了幾個值得注意的18世紀和19世紀的數學家，如拉格朗日和拉普拉斯，擴展和推廣了微擾理論的方法。採用這些發展良好的擾動方法，適應20世紀原子和亞原子物理學量子力學發展過程中出現的新問題。保羅·迪拉克（Paul Dirac）在1927年開發了擾動理論來評估粒子在放射性元素中的發射。後來被命名為費米的黃金法則。
行星運動研究的起點：
由於行星彼此非常遙遠，由於與太陽的質量相比，它們的質量很小，所以行星之間的重力可以忽略不計，行星運動被認為是第一次逼近，因為發生了沿著克卜勒的軌道，它們是由兩體問題的方程定義的，兩個物體是行星和太陽。
由於天文數據以更高的準確度得知，因此有必要考慮太陽周圍的行星的運動如何受到其他行星的影響。這是三體問題的起源；因此，在研究月球 - 月球系統的月球與地球之間的質量比被選為小參數。拉格朗日和拉普拉斯是第一個提出這樣的觀點，即描述星球在太陽周圍的運動的常數被“擾亂”，就像其他行星的運動一樣，隨著時間的推移而變化;因此稱之為“微擾理論”。
微擾理論由經典學者拉普拉斯，泊松，高斯進行了調查，結果可以以非常高的精度執行計算。根據行星天王星行動的偏差，他在1848年發現了海王星的行星，他是基於行星天王星的偏差（他將坐標傳遞給通過望遠鏡成功觀察海王星的約翰·戈特弗里德·加勒），代表了微擾理論的勝利。
擾動秩序
微擾理論的標準說明是以擾動的順序為依據：一階擾動理論或二階擾動理論，以及擾動狀態是否退化，這需要奇攝動。 在單一的情況下，理論稍微複雜一點。
在化學
許多從頭開始的量子化學方法直接使用微擾理論或者是密切相關的方法。 隱性微擾理論從一開始就與完整的哈密爾頓運算元一起工作，從未指定一個微擾運算元。 Møller-Plesset擾動理論使用Hartree-Fock哈密爾頓運算元和確切的非相對論哈密爾頓運算元之間的差異作為擾動。 零級能量是軌道能量的總和。 一階能量是Hartree-Fock能量，電子相關性包括在二階以上。 計算二階，三階或四階非常常見，代碼包含在大多數從頭開始的量子化學程式中。 相關但更準確的方法是耦合簇方法。
