微分環(differential ring)是帶導子集的環。若環R有一個導子集合Δ,則Δ稱為R的微分系,R稱為有微分系Δ的環,或簡稱微分環或Δ環。設S是有微分系Δ的環R的子環,若S也是有微分系Δ的環,則S稱為R的微分子環,或Δ子環,而R稱為S的微分擴環。
基本介紹
- 中文名:微分環
- 外文名:differential ring
- 領域:數學
- 學科:環論
- 定義:帶導子集的環
- 別稱:Δ環
概念


導子
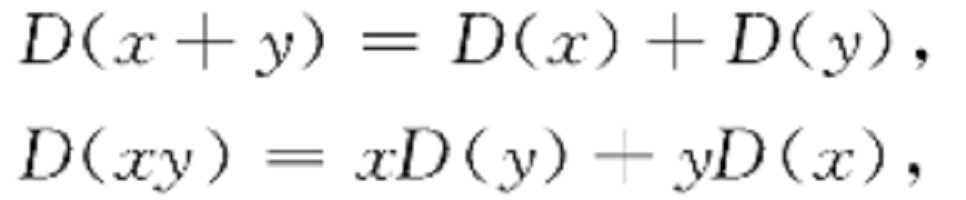
環

微分

微分環(differential ring)是帶導子集的環。若環R有一個導子集合Δ,則Δ稱為R的微分系,R稱為有微分系Δ的環,或簡稱微分環或Δ環。設S是有微分系Δ的環R的子環,若S也是有微分系Δ的環,則S稱為R的微分子環,或Δ子環,而R稱為S的微分擴環。


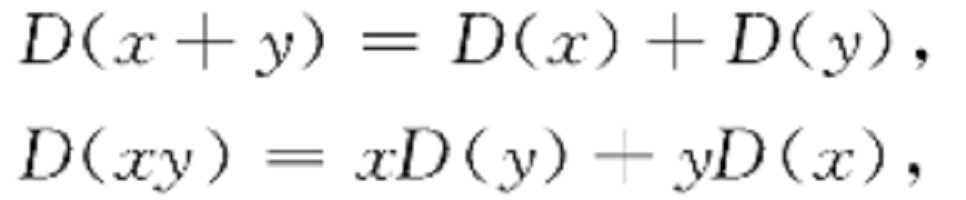


微分環(differential ring)是帶導子集的環。若環R有一個導子集合Δ,則Δ稱為R的微分系,R稱為有微分系Δ的環,或簡稱微分環或Δ環。設S是有微分系Δ的環R...
微分環節是控制系統的一類典型環節,微分環節的輸出量與輸入量對時間變數的導數值成比例。微分作用反映其輸入信號的變化速率.,因此,將微分環節引入控制系統中,可使...
環是對並與差運算封閉的集類,測度論中重要概念之一。設F是Ω上的一個非空集類。如果它對集的並及差運算封閉,即對任何A,B∈F,都有A∪B∈F,A\B∈F,則...
微分控制器是指僅具有微分控制作用的控制器。其控制規律是在一定界限內控制作用}t}變化量與輸入偏差的變化速度(即對時間的導數)成比例,是一個純微分環節。...
速度環運算是伺服電機運動控制的一環。運動伺服一般都是三環控制系統,從內到外依次是電流環、速度環、位置環。速度環的輸入就是位置調節後的輸出以及位置設定的前饋...
不同的自動控制系統,其物理結構不同,但從系統的數學模型來看,一般可將自動控制系統看作由若干個典型環節(比例環節、慣性環節、積分環節、微分環節、振盪環節以及時滯...
自動控制系統可分為開環控制系統和閉環控制系統。一個控制系統包括控制器﹑感測器...在工程實際中,套用最為廣泛的調節器控制規律為比例、積分、微分控制,簡稱PID控制...
線性控制系統(見線性系統)的典型環節主要有比例環節、積分環節、微分環節、慣性環節和振盪環節五種。表中列出各個典型環節的基本特性:輸入(用x表示)輸出(用y表示)...
2.5.1閉環控制系統的開環傳遞函式2.5.2自動控制系統閉環傳遞函式的求取2.5.3閉環系統的誤差傳遞函式2.6用Matlab求解微分方程和化簡系統框圖2.6.1系統傳遞函式模型...
第四節 套用拉氏變換求解微分方程本章小結思考題與習題第三章 自動控制系統的...第二節 可逆系統中的環流第三節 邏輯無環流可逆調速系統第四節 直流調速系統...
5.2.5 微分環節5.2.6 振盪環節5.2.7 二階微分環節5.2.8 不穩定環節5.2.9 延遲環節5.3 系統開環頻率特性的繪製5.3.1 最小相位系統和非最小相位...
5.2.1比例環節5.2.2積分環節和微分環節5.2.3慣性環節和一階微分環節5.2.4振盪環節5.2.5二階微分環節5.2.6延遲環節5.3開環系統的伯德圖...
4.3.8二階微分環節864.4系統開環頻率特性864.4.1系統的開環Bode圖的繪製864.4.2系統開環Nyquist圖的繪製884.4.3開環頻率特性與閉環系統性能的關係89...
5.2.3微分環節5.2.4慣性環節5.2.5一階微分環節5.2.6振盪環節5.2.7二階微分環節5.2.8延時環節5.3系統開環頻率特性的繪製...
4.2.5 一階微分環節854.2.6 振盪環節854.2.7 一階不穩定環節874.2.8 延遲環節874.3 系統開環對數頻率特性的繪製884.3.1 利用疊加法繪製系統開環對數頻率特性...
