對空間曲線而言,空間曲線在某點的單位切向量和副法向量所張成的平面為空間曲線的從切平面。對研究空間曲線的性質有著重要意義。
基本介紹
- 中文名:從切平面
- 外文名:Rectifying Plane
- 性質:關於單位切向量和副法向量的平面
- 套用:空間曲線的基本三棱形
一、從切平面定義

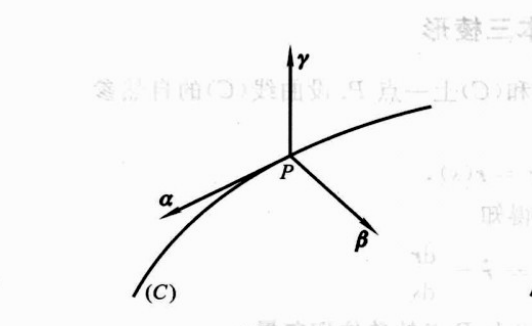 空間曲線的基本向量
空間曲線的基本向量





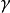
二、從切平面方程
1、自然參數方程
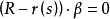

2、一般參數方程

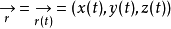

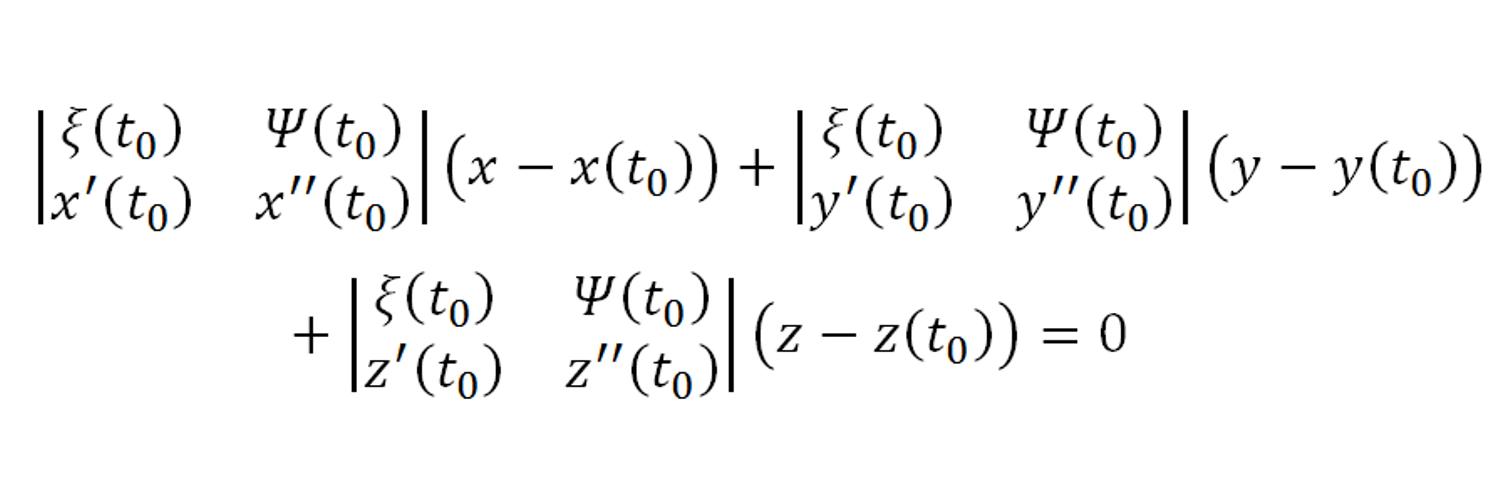
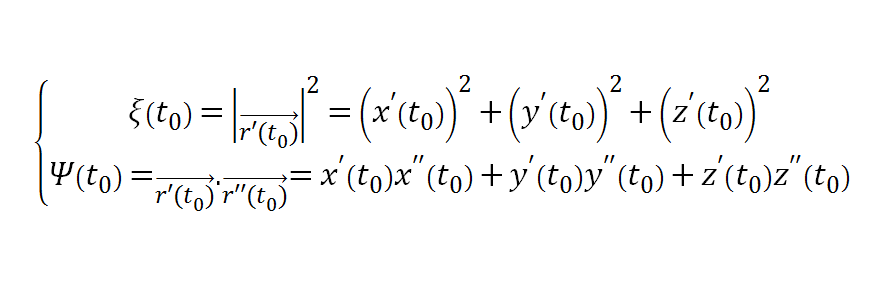
三、計算實例




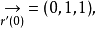

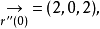


四、性質及意義
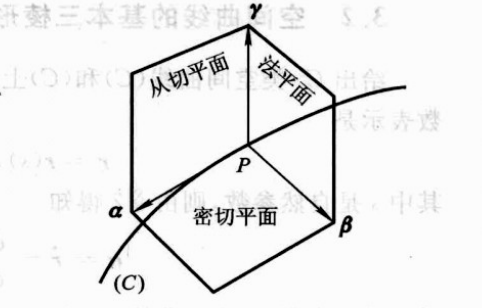 空間曲線的基本三棱形
空間曲線的基本三棱形
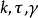
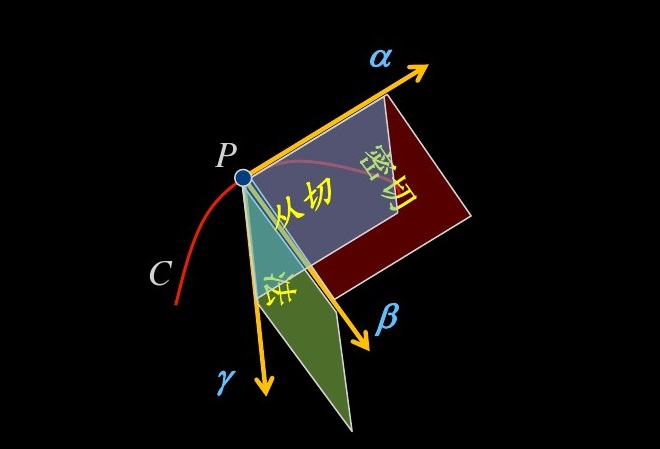
對空間曲線而言,空間曲線在某點的單位切向量和副法向量所張成的平面為空間曲線的從切平面。對研究空間曲線的性質有著重要意義。

 空間曲線的基本向量
空間曲線的基本向量





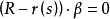


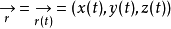

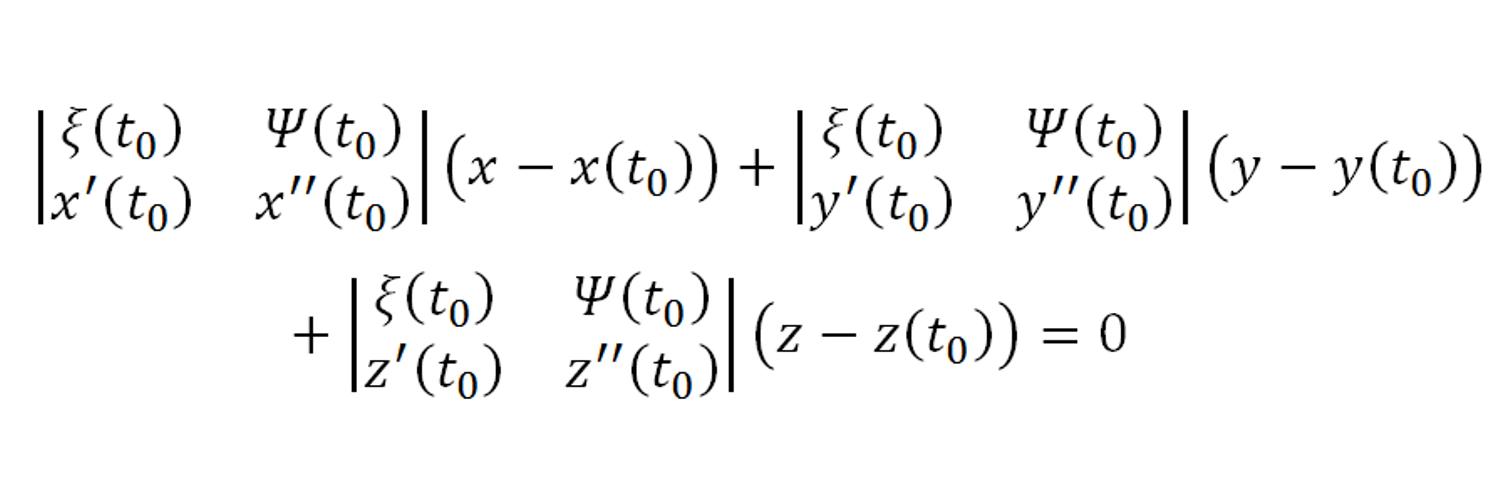
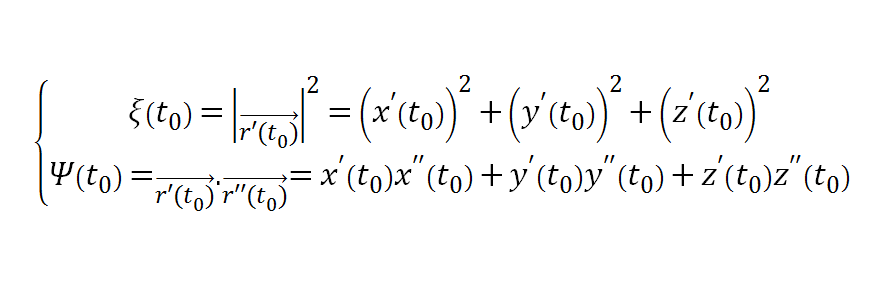




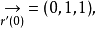

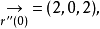


 空間曲線的基本三棱形
空間曲線的基本三棱形
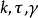
對空間曲線而言,空間曲線在某點的單位切向量和副法向量所張成的平面為空間曲線的從切平面。對研究空間曲線的性質有著重要意義。...
對於空間曲線而言,過曲線上一點有無數多個切平面,其中有一個最貼近曲線的切平面,被稱為密切平面,它在討論曲線的性質時有很重要的作用。...
這時從切平面上量得的量對於曲面來說就是內蘊幾何的量。這種把曲面小片看作平面的可能性是定義內蘊幾何的所有概念的基礎。作為例子,我們來討論角和面積的定義....
切平面到曲面的一種映射.設TP是曲面S在P點的切平面,指數映射是從切平面TP到曲面S上的一個對應關係,記成exp:TP→S,定義如下:設v是曲面S在P點的一個切向量...
一個平面σ,σ的極限位置稱為曲線C在p點的密切平面,它在p點的法線稱為曲線C在p點的次法線,曲線C在p點的切線和次法線決定的平面稱為曲線C在p點的從切平面...
一個平面σ,σ的極限位置稱為曲線C在p點的密切平面,它在p點的法線稱為曲線C在p點的次法線,曲線C在p點的切線和次法線決定的平面稱為曲線C在p點的從切平面...
一個平面σ,σ的極限位置稱為曲線C在p點的密切平面,它在p點的法線稱為曲線C在p點的次法線,曲線C在p點的切線和次法線決定的平面稱為曲線C在p點的從切平面...
一個平面σ,σ的極限位置稱為曲線C在p點的密切平面,它在p點的法線稱為曲線C在p點的次法線,曲線C在p點的切線和次法線決定的平面稱為曲線C在p點的從切平面...
一個平面σ,σ的極限位置稱為曲線C在p點的密切平面,它在p點的法線稱為曲線C在p點的次法線,曲線C在p點的切線和次法線決定的平面稱為曲線C在p點的從切平面...
