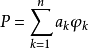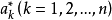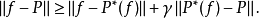強惟一性定理

強惟一性定理是惟一性定理的強化。惟一性定理是闡明每個連續函式僅有一個最佳逼近廣義多項式的定理。

基本介紹

• 中文名：強惟一性定理
• 外文名：strong uniqueness theorem
• 適用範圍：數理科學

簡介

強惟一性定理是惟一性定理的強化。

設函式組在[a,b]上滿足哈爾條件，f∈C[a,b]。若P*(f)是f關於Φ中的最佳逼近廣義多項式，則存在僅與f有關的常數γ>0，使得對任一關於中的廣義多項式P，都有

惟一性定理

惟一性定理是闡明每個連續函式僅有一個最佳逼近廣義多項式的定理。

設，φ_k∈C[a,b]。若Φ在[a,b]滿足哈爾條件，則對每個f∈C[a,b]，其關於Φ的最佳逼近廣義多項式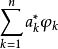是惟一的；若對每個f∈C[a,b]，其關於Φ的最佳逼近廣義多項式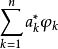是惟一的，則Φ在[a,b]上滿足哈爾條件。

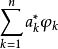
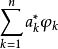
這一結論是哈爾(Haar,A.)於1918年建立的，所以常稱它為哈爾惟一性定理。

最佳逼近廣義多項式

(generalized polynomials of best approximation)

最佳逼近廣義多項式是指達到最佳逼近的廣義多項式。設，φ_k∈C[a,b]，若存在關於Φ的廣義多項式

使得

則稱P*(f)為f關於Φ的最佳逼近廣義多項式。

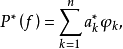
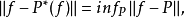
這裡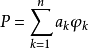是關於Φ的廣義多項式，a_k及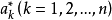都是實數。