基本介紹
眾所周知,線性回歸擬合時使用的是
最小二乘法,即保證各實測點至直線縱向距離的平方和為最小,這就帶來了一個問題:如果存在異常點或離群值,它們離回歸直線較遠,相應距離的平方就非常的大,為了保證平方和為最小,回歸直線不得不強烈的向該點所在方位偏移,顯然,這可能會導致錯誤的分析結論。因此,在回歸分析中必須要仔細考慮有無強影響點存在,在樣本量比較小的時候尤其應注意該問題。
強影響點是指保留該點與刪除該點2種情況下建立的
回歸方程中的回歸係數會產生很大差異的點。
一般稱嚴重偏離既定模型的數據點為異常點,遠離數據主體的點為高槓桿點,對統計推斷影響特別大的點為強影響點。其中異常點和高槓桿點都有可能形成強影響點。
強影響點的診斷
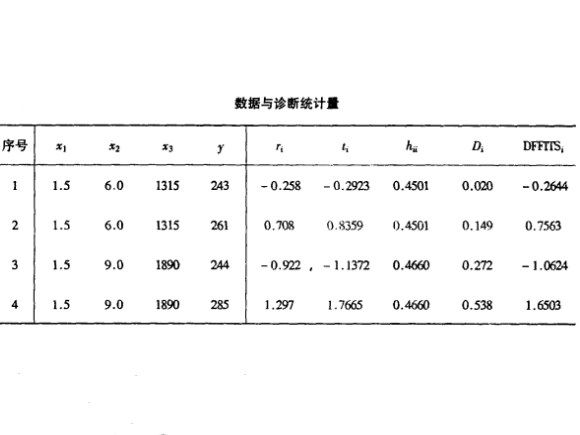
常用的診斷統計量有:
(1)描述性統計量。設投影陣的對角元為
,
的值越大,則第i點對回歸係數的估計的影響越大(也稱該點為槓桿點);
(2)採用Cook距離。
,式中
是第i點的標準化殘差,該值越大,則第i點對
回歸係數的估計的影響越大;
(3) W-K統計量。
,式中
是第i點的外學生化殘差,該值越大,則第i點對回歸係數的估計的影響越大。
若某點為異常點,它可能是強影響點,但也可能不是強影響點,同樣,強影響點可能是異常點,也可能不是。
當具有異常點或強影響點時,避免它對於估計和擬合的影響的一種方法是刪除該點後建立回歸方程。
SPSS中對強影響點的診斷有以下幾種方法:
1.做出散點圖,觀察有無離群值,它們往往就是強影響點。需要注意的是有些觀察值在各個變數單獨描述時處在正常範圍內,但幾個變數聯合描述則為異常,例如年齡10歲和體重70公斤單獨存在時都不奇怪,但如果同一個人年齡10歲並且體重70公斤顯然就不正常了。
2.使用Statistic子對話框中的殘差診斷指標,如果殘差非常大,則相應數據離回歸直線較遠,可能為強影響點。
3.使用Save子對話框中的距離指標和專門的影響力統計量。相應的指標和標準請參見Linear過程的界面說明。
4.採用穩健回歸方法。對
線性回歸模型進行診斷時,如果存在多個異常點,使用以上方法容易發生掩蓋現象,即未能識別真正的異常點。此時,我們應該考慮採用基於穩健估計的診斷方法。穩健回歸方法本身是為了減少異常值對估計值的擾動,屬於診斷後的治療措施。但同時它也可以作為識別異常點的工具。
對強影響點的處理對策
如果確認存在強影響點,首先應當做的工作是檢查原始記錄,看看是不是數據錄入錯誤。如果確認數據無誤,則分析中可能採取的策略有:
去除:如果只有一兩個強影響點,可以考慮將其不納入分析,以確保分析結果能夠代表大多數數據的特徵。畢竟統計分析是一個
少數服從多數的民主過程,可以在分析報告後對這幾個強影響點進行單獨描述,以全面概括樣本信息。
變數變換:採用適當的變數變換方法可能會消除強影響點的存在,如倒數變換、對數變換等。這些方法的實質就是弱化極端值的離群趨勢,把這些異己分子拉回到集體中來。
非參數分析:可以考慮對存在強影響點的變數求秩次,然後採用秩次代替原變數進行
回歸分析。這是秩分析思想的一種套用,在樣本量較大時非常有效。
最小一乘法:顧名思義,最小一乘法就是保證各實測點至直線縱向距離絕對值之和為最小,顯然比
最小二乘法對強影響點有更強的耐受力。該方法在SPSS中採用Nonlinear過程實現。
採用加權最小二乘法:利用Weight Estimation過程對強影響點賦予較小的權重,從而削弱對回歸方程的影響。這實際上是
穩健回歸(Robust Regression)思想的一種套用。由於
加權最小二乘法中需要找到能夠準確預測變異程度的指標,此處可以先進行普通的回歸分析,將
殘差存為新變數,然後將它指定為分析中的加權變數,這樣就可能較為準確的預測殘差,從而得到較滿意的方程。
異常點和強影響點的聯繫和區別
模型中“異常點"和“強影響點"的聯繫和區別
在幾乎所有統計診斷中,都將涉及兩個基本概念:異常點和強影響點。相關文獻對它們作了詳細的比較,需要強調的是,巨觀經濟數據的異常點和強影響點都是一個多維向量,而不是一個單獨的數據。這是因為經濟系統是一個相互聯繫、相互制約的整體,在衡量某一個經濟變數是否異常時,不能簡單地以它自己單獨作為判斷,同時還必須考慮與其相關的其他經濟變數是否能夠支撐經濟系統的平衡,結合巨觀經濟統計數據中的異常點和強影響點這兩個概念,下面再對二者作一些總結和說明。
異常點
在回歸模型中,異常點是指對既定模型偏離很大的數據點。但究竟偏離到何種程度才算是異常,這就必須對模型誤差項的分布有一定的假設(通常假定為
常態分配)。另外,儘管異常點的概念看起來很明顯,圖形上也很直觀,但要給它下一個精確的定義卻是相當困難的事情。事實上,至今尚無一個公認的統一定義。Bechman和Cook(1983)指出,對於異常點的理解一般有兩種情形:第一,子樣雖屬同一母體,但此值與其他值相比異常地離開,把異常點看成是那些與數據集的總體明顯不協調、小機率發生時所產生的數據點。這時,異常點可解釋為落在分布的單側或雙側
分位點以外的點。第二,把異常點視為雜質點(contaminant)。它與數據集的主體不是來自同一分布,是在絕大多數來自某一共同分布的數據點中摻入的來自另一分布的少量“雜質”。不管採用哪種看法,“異常點”的“異常”之處總是相對於數據集的總體或所假定的模型而言的。在回歸模型中,異常點對模型的偏離程度要遠比數據主體中的點大。
強影響點
數據集合中的強影響點是指那些對統計量的取值有非常大的影響的點。在分析影響大小時,有幾個基本問題需要考慮。首先必須明確是對哪一個統計量的影響?一般來講,對於既定模型,通常總是選擇幾個有興趣的統計量,然後考察數據點對它們的影響。其次必須確定度量影響的尺度是什麼?為了定量地刻畫影響的大小,迄今為止已提出多種尺度。例如,基於殘差的尺度、基於擬合的尺度、基於影響函式的尺度、基於置信域的尺度、基於似然函式的尺度等。在每一種類型中又可能有不同的統計量,例如基於影響函彭就已提出多種“距離”來度量,有cook距離、welsch-kuh距離、修正的cook距離等。可見,如何研究影響與從何種角度考慮統計問題有密切關係。每一種度量都是著眼於某一方面的影響,並在某種具體場合下較為有效。這一方面反映了度量影響問題的複雜性,在實際套用中,可以選擇幾種不同的度量對影響進行分析並對各種分析結果加以比較,以期待得到更為全面的結論。這裡需要強調和說明的是,巨觀經濟統計數據中的強影響點研究的前提條件是建立在正確的
計量經濟模型基礎上的,因此模型的設定除了一般統計模型所必須的條件要求外,同時還必須具有明確的經濟意義。
如同對待異常點的處理一樣,對已判定的強影響點必須慎重處理。強影響點通常是數據集合中更為重要的數據點,它往往能提供比一般數據點更多的信息,因此須引起特別注意。同時,強影響點和異常點是兩個不同的概念,它們之間有一定的聯繫,也有區別。強影響點可能同時又是異常點也可能不是;反之,異常點可能同時又是強影響點也可能不是。