加權最小二乘法

加權最小二乘法是對原模型進行加權，使之成為一個新的不存在異方差性的模型，然後採用普通最小二乘法估計其參數的一種數學最佳化技術。

基本介紹

• 中文名：加權最小二乘法
• 外文名：weighted least square method
• 實質：數學最佳化技術
• 方式：最小化誤差的平方和
• 所屬學科：數學

定義

一般最小二乘法將時間序列中的各項數據的重要性同等看待，而事實上時間序列各項數據對未來的影響作用應是不同的。一般來說，近期數據比起遠期數據對未來的影響更大。因此比較合理的方法就是使用加權的方法，對近期數據賦以較大的權數，對遠期數據則賦以較小的權數。加權最小二乘法採用指數權數W^n-i，0<W<1，加權以後求得的參數估計值應滿足：

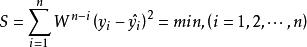
以直線模型 為例，其加權的剩餘平方和為：

對上式分別求a和b的偏導數，得到標準方程組：

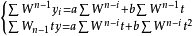
對上述方程解出a和b，就得到加權最小二乘法直線模型。套用加權最小二乘法，W的取值不同，解出的a，b也不同，因此W值取多少，需要經分析後確定。

疊代加權最小二乘法

假設用作Ω對角線值倒數的個體方差未知，且不能被輕易估計，但已知它們是結果變數均值的一個函式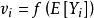： 。那么，如果結果變數的期望值E[Y_i]=μ和關係函式的形式f()是已知的，這就是一個非常直觀的估計過程。不幸的是。儘管方差結構與均值函式的相關性非常普遍，但是相對來說，我們不太知道這一相關的確切形式。

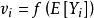
這個問題的一個解決方法是疊代地估計權重，在每一輪估計中用均值函式提升估汁。因為 ，因此係數估計 提供了一個均值估計，反過來也是一樣。因此算法用漸進提升的權重來疊代估計這些量。過程如下：

1．為權重設定起始值，一般等於1(也就是沒有權重的回歸)：1/v_i⁽¹⁾=1，並且構建對角線矩陣Ω，防止以零做除數。

2．以現有的權數用加權最小二乘法估計β。第j個估計是： 。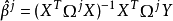

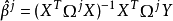
3．用新估計的均值向量1/v_i^(j+1)=VAR(μ_i)更新權數。

4．重複第二步和第三步直到收斂(也就是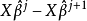 足夠接近於0)。

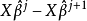
在滿足指數族分布的一般條件下，疊代加權最小二乘的程式得到似然函式的眾數，然後產生未知係數向量 的最大似然估計。進一步地．由 產生的矩陣與 的方差矩陣按照預期成機率收斂。

因為我們在廣義線性模型中確定了一個明確的連線函式，所以多元正態方程的形式可以修改為包括這一嵌入的轉化：

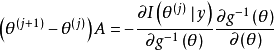
很明顯，線上性模型的情況下，當連線僅僅是恆等函式時，上述方程就可以簡化。對於廣義線性模型，IWLS操作的總體策略相當簡單：用費歇得分的牛頓--萊福遜算法反覆地套用於修正的上述常規方程。對於精闢細緻的分析和這一操作的擴展，讀者可以參看格林(Green．1984)和德爾皮諾(del Pino，1989)的論述。

加權最小二乘法估計

考慮各個觀測數據誤差分布的不同，定義加權目標函式

式中W是加權矩陣，為S×S階對稱正定矩陣。

將 代入式(1)，並令

可解得加權最小二乘估計

加權矩陣W的取法值得討論。可以證明，如果ε是具有零均值的平穩隨機過程，且與叉 、 無關，則 是無偏估計，但不是有效估計和一致估計。W取特定值時， 才能成為有效估計。

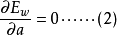
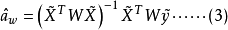
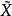
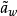
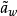
設a是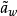 估計的真值，估計誤差 的協方差矩陣

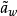
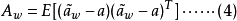
將 代入到式(3)中，得

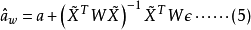
將式(5)代入到式(4)中，整理得

其中

式中C是殘差ε的協方差矩陣。

可以證明，若取加權矩陣

則是A_w範數最小，記為A_MV。式(8)代入(6)，得

此時系統參數加權最小二乘估計 為有效估計，稱為馬爾可夫估計，記為 。式(8)代入式(3)，得馬爾可夫估計為：

因為馬爾可夫估計是無偏有效估計，所以一般加權最小二乘法均指馬爾可夫估計。此外，如果殘差ε為獨立、同分布、均值為零的隨機矢量，設方差為σ²，即

式中I為單位矩陣。

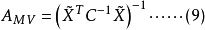
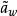
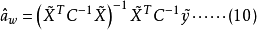
易知最小二乘法估計誤差協方差A與馬爾可夫估計誤差協方差A_MV相等，即A=A_MV。因此，選用權矩陣

此時，馬爾可夫估計 與最小二乘法估計 相等，即 。

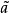
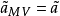
舉例

通過最小二乘法擬合線性趨勢方程。

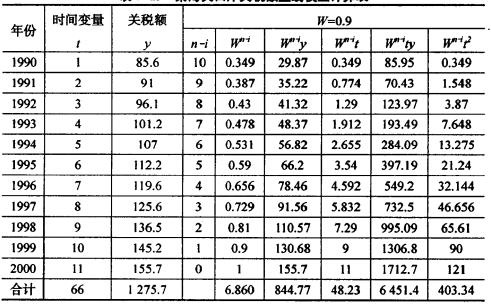某海關口岸關稅額直線模擬計算表

將表中數據代入公式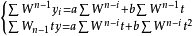

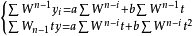
得： ，解得a=66.95，b=8；所得趨勢方程為：

比較兩種估計方法的結果(具體數據見下表)，可以看出，加權最小二乘法的近期誤差比遠期誤差小，這就是加權最小二乘法的優勢所在。

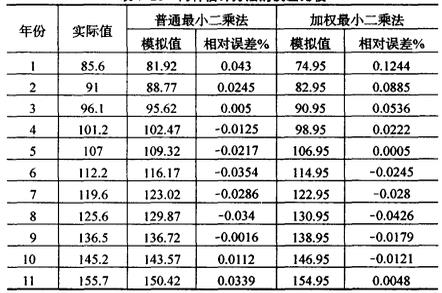兩種估計方法的誤差比較