基本介紹
- 中文名：高槓桿點
- 外文名：high leverage case
- 所屬學科：數學（統計學）
- 定義：自變數因子空間中的離群點
- 相關概念：槓桿統計量、離群點、多元回歸等
基本介紹,多元回歸中高槓桿點的辨認,異常點與強影響點,
基本介紹
離群點是指對於給定的預測值
來說，回響值
異常的點。相反，高槓桿(high leverage) 表示觀測點是異常的。例如，圖1(a)左圖中的觀測點41具有高槓桿值，因為它的預測變數值比其他觀測點都要大。實線是對數據的最小二乘擬合，而虛線是刪除觀測點41後的擬合。事實上，高槓桿的觀測往往對回歸直線的估計有很大的影響。如果一些觀測對最小二乘線有重大影響，那么它們值得特別關注，這些點出現任何問題都可能使整個擬合失效。因此找出高槓桿觀測是十分重要的。
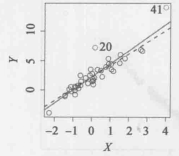
圖1（a）
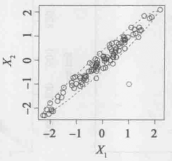
圖1（b）
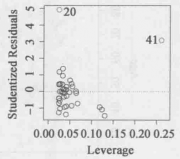
圖1（c）
圖1(a)：觀測點41是一個高槓桿點，而點20不是。實線是對所有數據的擬合，虛線是去掉觀測點41後的擬合。(b): 遠離的觀測點的
值或
值並非不尋常，但它仍落在數據主體之外，因此是高槓桿點。(c): 觀測點41具有高槓桿值和高殘差。
多元回歸中高槓桿點的辨認
在簡單線性回歸中，高槓桿觀測是很容易辨認的，我們可以簡單地找到預測變數的取值超出正常範圍的觀測點。但是，在有許多預測變數的多元線性回歸中，可能存在這樣的觀測點：單獨來看，它各個預測變數的取值都在正常範圍內，但從整個預測變數集的角度來看，它卻是不尋常的。圖1（b）的圖就是一個例子，它反映了一個有兩個預測變數和的數據集。其中大多數觀測的預測變數值都在虛線劃出的橢圓範圍內，而有一個的觀測點在橢圓之外。但此點的和的值都是正常的。因此，如果我們只檢查和將無法發現這種高槓桿點。在有兩個以上的預測變數的多元回歸中，這個問題更加明顯，因為這種情況下沒有簡單的方法可以同時繪製數據的所有維度。為了量化觀測的槓桿作用，可以計算槓桿統計量(leverage statistic)。一個大的槓桿統計量對應一個高槓桿點。對於簡單線性回歸，有
圖1(c)圖提供了與學生化殘差的關係圖，所用的是圖1(a)中的數據。觀測41脫穎而出是因為它的槓桿統計量和學生化殘差都很高。換句話說，它既是離群點，又是高槓桿點。這是一個特別危險的組合。
異常點與強影響點
線性回歸尤其是多因素回歸分析過程中，要保證模型建立得合理、科學，模型診斷(model diagnosis) 是必不可少的。所謂模型診斷主要是檢查數據是否符合線性回歸的套用條件，變數間是否存在多重共線性(multicollinearity)，是否存在異常點或強影響點等。
異常點檢查 異常點主要包括離群點(outliers) 和高槓桿點(high leveragepoints)。離群點是指殘差與其他點相比較大的點，是針對因變數而言。高槓桿點通常指自變數中出現的異常點。強影響點(influential points) 是指對模型有較大影響的點，模型中包含該點與不包含該點會使求得的回歸係數相差很大。如果某點既是離群點又是高槓桿點，則該點很有可能是強影響點，
(1) 離群點在SAS 輸出中可通過學生化殘差(student residual)來判斷。如果學生化殘差絕對值
，可以認為是一個可疑點；如果學生化殘差絕對值
，基本可以認定是一個離群點。
(3) 強影響點的診斷指標主要有Cook距離(Cook's D)，它綜合反映了槓桿值和殘差大小。Cook'sD值大，表明所對應的觀測點的自變數和因變數均為異常值，對模型有較大影響。
(4) 強影響點的另一個診斷指標是DFFITS。它反映了變數的影響大小，表示某個樣品被刪除後模型的變化。變化越大(即DFFITS值越大)，表明該觀測值的影響越大。
提示：並非所有的異常點都意味著結果不好，有時候發現異常點可能會提示有更重要的信息。如果出現異常點，首先應檢查數據是否錄入錯誤，也可以選擇其他相應模型來擬合，或者需要收集更多的數據來證實。
