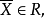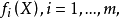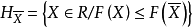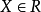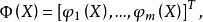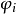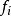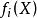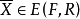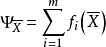弱有效解(weakly efficient solution)亦稱帕雷托弱有效解,是多目標規劃的基本概念之一。
基本介紹
- 中文名:弱有效解
- 外文名:weakly efficient solution
- 別名:帕雷托弱有效解
- 所屬學科:數學
- 所屬領域:運籌學(多目標規劃)
- 相關概念:多目標極小化模型、有效解等
定義,相關性質定理,定理1,定理2,定理3,定理4,判別準則與存在性,定理1,定理2,定理3,定理4,定理5,定理6,
定義


上述定義表明,在向量不等式“<”的意義下,在問題(VMP)的約束集中已找不到比弱有效解更好的解。模型(VMP)的全部弱有效解所組成集合叫做模型( VMP) 的弱有效解集,記作 或簡記為
或簡記為 。
。


相關性質定理
下面定理1反映了向量目標函式經過一個單調變換之後,對應的多目標極小化模型的有效解(或弱有效解)和原模型的有效解(或弱有效解)之間的關係。
定理1
(1)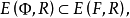
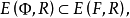
(2) 。
。

定理2
模型(VMP)的有效解一定是弱有效解。
由有效解和弱有效解的定義直接可證。
定理3
對模型(VMP),若絕對最優解集 ,則有效解集與絕對最優解集相同,即E(F,R)=E*(F,R)。
,則有效解集與絕對最優解集相同,即E(F,R)=E*(F,R)。

定理4
判別準則與存在性
下面介紹判別有效解和弱有效解的基本準則,並利用它們來討論有效解和弱有效解的存在性問題。為此,引進一個與模型(VMP)有關的如下輔助問題:
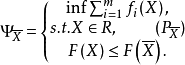
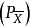

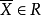
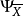
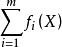
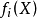
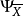
定理1
定理2
設模型(VMP)的約束集為R,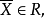 且
且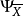 為有限的,若
為有限的,若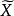 是
是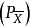 的最優解,則
的最優解,則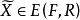 。
。
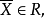
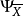
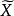
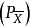
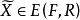
定理3
設模型(VMP)的約束集為R,則
(1) 當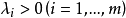 時,若
時,若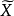 是
是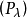 的最優解,則
的最優解,則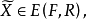 即
即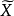 是模型(VMP)的有效解。
是模型(VMP)的有效解。
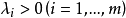
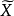
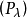
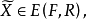
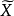
(2) 當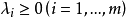 時,且至少有一個為嚴格不等式,若
時,且至少有一個為嚴格不等式,若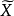 是
是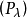 的最優解,則
的最優解,則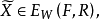 即
即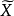 是模型(VMP)的弱有效解。
是模型(VMP)的弱有效解。
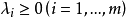
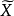
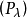
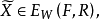
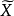
定理4
設模型(VMP)的約束集為R,則
(1) 當 關於
關於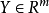 是嚴格增函式時,若
是嚴格增函式時,若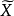 是
是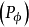 的最優解,則
的最優解,則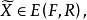 即
即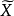 是模型(VMP)的有效解。
是模型(VMP)的有效解。

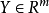
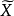
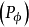
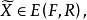
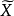
(2) 當 關於
關於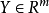 是增函式時,若
是增函式時,若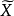 是
是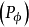 的最優解,則
的最優解,則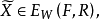 即
即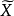 是模型(VMP)的弱有效解。
是模型(VMP)的弱有效解。

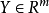
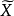
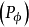
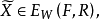
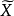
下面給出有效解的兩個存在性條件。
定理5
設模型(VMP)的約束集為R,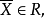 且
且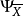 有限,若下列極小化問題
有限,若下列極小化問題
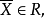

定理6