設F(R) 表示R中所有X應的P維向量F(X)的全體,即F(R)={F(X)|X∈R),如果把F(X)看作是從約束集合R到Ep的映射,則F(R)稱為象集或目標空間,R稱為原象集或策略空間。
基本介紹
- 中文名:象集
- 外文名:image set
- 別稱:目標空間
- 所屬學科:數學
- 相關概念:目標規劃、原象集、有效點等
定義,有效點與弱有效點,相關定理,定理1,定理2,
定義
考慮多目標規劃問題:
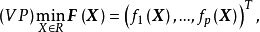

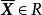


定義1 設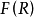 表示R中所有X應的P維向量F(X)的全體,即F(R)={F(X)|X∈R),如果把F(X)看作是從約束集合R到Ep的映射,則F(R)稱為象集或目標空間,R稱為原象集或策略空間。
表示R中所有X應的P維向量F(X)的全體,即F(R)={F(X)|X∈R),如果把F(X)看作是從約束集合R到Ep的映射,則F(R)稱為象集或目標空間,R稱為原象集或策略空間。
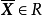
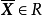



有效點與弱有效點
類似於約束集R中的有效解和弱有效解,下面定義象集F(R)中的有效點和弱有效點。
定義2 設 ,若不存在
,若不存在 ,使
,使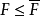 成立,則
成立,則 稱為象集
稱為象集 的有效點,有效點的全體記作
的有效點,有效點的全體記作 。
。


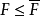



定義3 設 ,若不存在
,若不存在 ,使得
,使得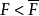 成立,則稱
成立,則稱 為象集
為象集 的弱有效點,弱有效點的全體記作
的弱有效點,弱有效點的全體記作 。
。





研究象集的作用在於:
(1)求出了 的有效點和弱有效點,就可以確定
的有效點和弱有效點,就可以確定 的有效解和弱有效解。
的有效解和弱有效解。


(2)對象集的研究可以提供一些解多目標規劃的方法。
(3)可以從幾何上(p=2)對一些常用的解法加以解釋。
相關定理
有效解和有效點,弱有效解和弱有效點之間有如下的關係:
定理1
若已知象集 的有效點集
的有效點集 ,則
,則 的有效解集
的有效解集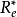 為:
為: 。
。



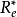

證明: 設 ,則存在
,則存在 ,使得
,使得 ,要證
,要證 ,用反證法。設
,用反證法。設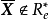 ,則存在
,則存在 ,使
,使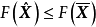 ,令
,令 ,知
,知 且
且 ,這與
,這與 矛盾,故有
矛盾,故有 。定理證畢。
。定理證畢。




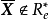

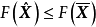





類似地可以證明下面定理。
定理2
若已知象集 的弱有效點集
的弱有效點集 ,則
,則 的弱有效解集
的弱有效解集 為:
為: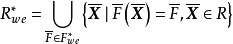




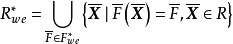
這兩個定理說明, 的有效點和弱有效點的原象分別為
的有效點和弱有效點的原象分別為 的有效解和弱有效解。
的有效解和弱有效解。



