局部凸空間E的共軛空間E*的定向列{f(Aαx)|α∈Λ}稱為弱∗基本的,是指{fα|α∈Λ}按E*中的弱∗拓撲是基本定向列。
基本介紹
- 中文名:弱∗基本定向列
- 外文名:strong ∗ fundamental directed set of points
- 適用範圍:數理科學
簡介,弱∗拓撲,弱基本定向列,
簡介
弱∗基本定向列是在弱∗拓撲意義下的基本定向列。
局部凸空間E的共軛空間E*的定向列{f(Aαx)|α∈Λ}稱為弱∗基本的,是指{fα|α∈Λ}按E*中的弱∗拓撲是基本定向列,即對任何x∈E,{f(Aαx)|α∈Λ}是基本定向列。
弱∗拓撲
設線性空間對(X,Y)關於雙線性泛函〈·,·〉成為對偶,稱X上由半範數族{|〈·,y〉||y∈Y}確定的局部凸拓撲為X的關於對偶Y的弱拓撲,記為σ(X,Y)。對稱地,Y上由半範數族{|〈x,·〉||x∈X}確定的局部凸拓撲稱為Y的關於對偶X的弱拓撲,記為σ(Y,X)。當X為局部凸空間時,(X,X)為自然對偶,σ(X,X)稱為X的弱拓撲,而σ(X,X)稱為X的弱∗拓撲。相應地,X中原有的拓撲稱為強拓撲。
弱基本定向列
局部凸空間E中的定向列{xα|α∈Λ}稱為強(弱)基本的,是指{xα|α∈Λ}依強(弱)拓撲是基本的,即對任一給定的強(弱)鄰域U,存在α0,當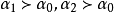 時,總有
時,總有 。
。
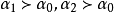

對於有界線性運算元空間𝓑(X→Y)(其中X,Y是賦范線性空間),𝓑(X→Y)中運算元定向列{Aα|α∈Λ}是強(弱)基本的充分必要條件是:對每個x∈X,{Aαx|α∈Λ}是Y中的強(弱)基本定向列。
