基本介紹
- 中文名:延森不等式
- 外文名:Jensen's inequality
- 學科:數學
- 又名:琴生不等式
一般形式
測度論的版本


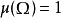
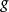
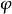
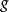

機率論的版本
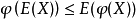
機率密度函式的形式


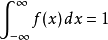
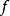

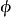







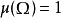
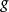
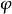
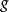

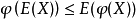


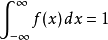
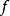

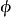




延森不等式(也譯作琴生不等式)以丹麥數學家約翰·延森(Johan Jensen)命名。它給出積分的凸函式值和凸函式的積分值間的關係。延森不等式有以下推論:過一個凸函式...
吉布斯不等式是由約西亞·吉布斯在19世紀提出的。在資訊理論和機率論中,它能套用在Fano不等式和訊號源編碼定理的證明。...
凸性不等式(convexity inequality)是凸函式滿足的不等式,也常稱為延森不等式。...... 凸性不等式(convexity inequality)是凸函式滿足的不等式,也常稱為延森不等式...
積分不等式是微積分學中的一類重要不等式,也為解決微分方程等方面的問題提供了 富有成效的理論工具。主要有楊不等式,施瓦茲不等式,閔可夫斯基不等式,延森不等式等...
有延森不等式的關係,即與熱力學第二定律相一致。自從它被推導出來之後,Jarzynski恆等式已經在許多不同的領域內被證實,由生物分子的實驗到數值模擬。其他許多的推導也...
琴生不等式以丹麥技術大學數學家約翰·延森(Johan Jensen)命名。它給出積分的凸函式值和凸函式的積分值間的關係。琴生(Jensen)不等式(也稱為詹森不等式),使用時...
6)延森不等式[1] 對嚴格凸函式 f 都成立。7)如果 和 是嚴格凸函式,那么 和 也是嚴格凸函式。8) 如果 和 是嚴格凸函式,且 遞增,那么 是嚴格凸函式。...
6)反向延森不等式[2] 對嚴格凹函式 都成立。7)如果 和 是嚴格凹函式,那么 和 也是嚴格凹函式。8)如果 和 是嚴格凹函式,且g遞減,那么 是嚴格凹函式。...
延森不等式對於每一個凸函式f都成立。如果X是一個隨機變數,在f的定義域內取值,那么(在這裡,E表示數學期望。)凸函式還有一個重要的性質:對於凸函式來說,局部最...
算起.現今,人們熟知的柯西不等式、幾何平均不大於算術平均等,都起源於柯西利用函式的凸性來證明不等式的研究.系統的凸性不等式研究是延森(Jensen,J.L.W.V.)的...
