廣義回歸神經網路

在數學建模領域，徑向基函式網路（Radial basis function network，縮寫 RBF network）是一種使用徑向基函式作為激活函式的人工神經網路。徑向基函式網路的輸出是輸入的徑向基函式和神經元參數的線性組合，廣義回歸神經網是基於徑向基函式網路一種改進。廣義回歸神經網路也可以可以通過徑向基神經元和線性神經元來設計。

基本介紹

• 中文名：廣義回歸神經網路
• 外文名：general regression neural network(GRNN) 
• 學科：人工智慧
• 定義：基於徑向基函式網路一種改進
• 有關術語：徑向基函式
• 套用：時間序列預測、分類和系統控制

簡介

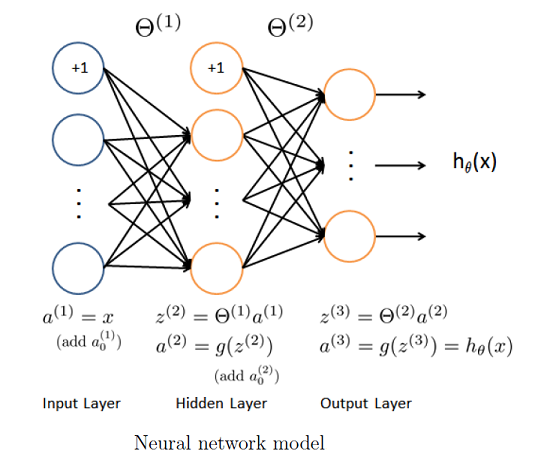
在機器學習和認知科學領域，人工神經網路（英文：artificial neural network，縮寫ANN），簡稱神經網路（英文：neural network，縮寫NN）或類神經網路，是一種模仿生物神經網路(動物的中樞神經系統，特別是大腦)的結構和功能的數學模型或計算模型，用於對函式進行估計或近似。神經網路由大量的人工神經元聯結進行計算。廣義回歸神經網路是建立在數理統計基礎上的徑向基函式網路，其理論基礎是非線性回歸分析。GRNN具有很強的非線性映射能力和學習速度，比RBF具有更強的優勢，網路最後普收斂於樣本量集聚較多的最佳化回歸，樣本數據少時，預測效果很好，網路還可以處理不穩定數據。一般可以通過徑向基神經元和線性神經元可以建立廣義回歸神經網路。

GRNN 在結構上由四層構成，分別為輸入層、模式層、 求和層和輸出層。輸入層神經元的數目等於學習樣本中輸入向量的維數， 各神經元是簡單的分布單元， 直接將輸入變數傳遞給模式層。模式層神經元數目等於學習樣本的數目n，各神經元對應不同的樣本。求和層中使用兩種類型神經元進行求和。輸出層中的神經元數目等於學習樣本中輸出向量的維數 k， 各神經元將求和層的輸出相除，經元 j 的輸出對應估計結果 Y (X) 的第 j 個元素。

徑向基函式網路

在數學建模領域，徑向基函式網路（Radial basis function network，縮寫 RBF network）是一種使用徑向基函式作為激活函式的人工神經網路。徑向基函式網路的輸出是輸入的徑向基函式和神經元參數的線性組合。

RBF神經網路的基本思想：用RBF作為隱單元的“基”構成隱藏層空間，隱藏層對輸入矢量進行變換，將低維的模式輸入數據變換到高維空間內，使得在低維空間內的線性不可分問題在高維空間內線性可分。

BF是具有單隱層的三層前向網路。第一層為輸入層，由信號源節點組成。第二層為隱藏層，隱藏層節點數視所描述問題的需要而定，隱藏層中神經元的變換函式即徑向基函式是對中心點徑向對稱且衰減的非負線性函式，該函式是局部回響函式，具體的局部回響體現在其可見層到隱藏層的變換跟其它的網路不同。以前的前向網路變換函式都是全局回響的函式。第三層為輸出層，是對輸入模式做出的回響。輸入層僅僅起到傳輸信號作用，輸入層和隱含層之間之間可以看做連線權值為1的連線，輸出層與隱含層所完成的任務是不同的，因而他們的學習策略也不同。輸出層是對線性權進行調整，採用的是線性最佳化策略，因而學習速度較快；而隱含層是對激活函式（格林函式，高斯函式，一般取後者）的參數進行調整，採用的是非線性最佳化策略，因而學習速度較慢。

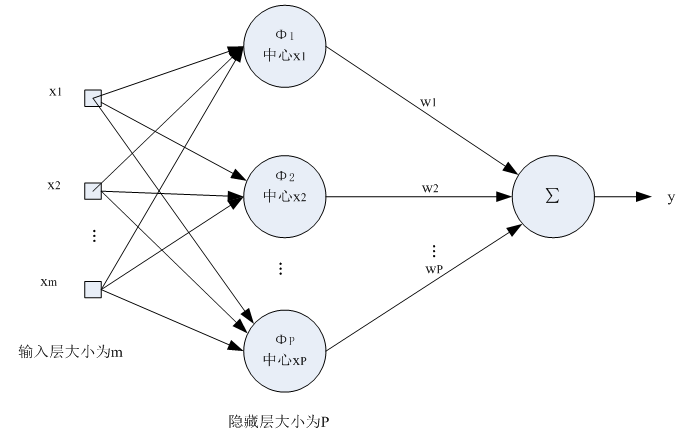
徑向基函式神經網路的優點：逼近能力，分類能力和學習速度等方面都優於BP神經網路，結構簡單、訓練簡潔、學習收斂速度快、能夠逼近任意非線性函式，克服局部極小值問題。原因在於其參數初始化具有一定的方法，並非隨機初始化。

徑向基函式

徑向基函式是一個取值僅僅依賴於離原點距離的實值函式，也就是Φ（x）=Φ(‖x‖),或者還可以是到任意一點c的距離，c點稱為中心點，也就是Φ（x，c）=Φ(‖x-c‖)。任意一個滿足Φ（x）=Φ(‖x‖)特性的函式Φ都叫做徑向基函式，標準的一般使用歐氏距離（也叫做歐式徑向基函式），儘管其他距離函式也是可以的。在神經網路結構中，可以作為全連線層和ReLU層的主要函式。

構造神經網路的基本方法為假設某種過程是屬於某種函式空間的函式，然後連線成神經格線，運行一段時間該網路的電勢趨於最小達到某種動態的平衡，從而可以求出該函式，而選擇徑向基函式空間是一個比較簡單的容易用神經網路實現的方法。

在B肝發病數時間序列預測中的套用

背景

近年來，國內廣泛展開了傳染病的早期預測預警的研究，對傳染病的發生、 流行及其變化趨勢的預測方法主要有回歸預測模型、 時間序列模型、 傳染病傳播動力學模型等方法。回歸預測以及傳播動力學模型的研究集中在對其因果關係的分析上，然而影響傳染病發病的因素眾多，所需的許多影響因素的數據難以收集，所建立的模型不能全面和本質地反映所要預測動態數據。基於時間序列的預測是一種較為簡單的傳染病預測方法，許多時間序列分析的模型等已經廣泛地套用於傳染病預測當中，如馬爾科夫鏈模型、 灰色預測模型、 自回歸移動平均模型等。其中，人工神經網路以其獨特的並行結構、 自適應、 自組織、 較強的容錯性、 魯棒性等特點和獨特的信息處理方法，在時間序列預測領域得到了廣泛的套用。

目前， 在預測時用的最多的是反饋 BP 神經網路 BPNN(Error Back Propagation neural network)模型， 但該模型在訓練時存在收斂速度慢和容易陷入局部極小的缺點，預測效果可能達不到預期效果廣義回歸神經網路GRNN(Generalized Regression Neural Network)。GRNN 收斂於樣本量積聚較多的最佳化回歸面，並且在樣本數據較少時， 預測效果也較好。因此，GRNN 在多個各個領域得到了較為廣泛的套用。然而它在傳染病預測領域的報導仍然較少。

B肝是一種典型的腸道傳染病， 呈現周期性流行特徵。B肝傳染性強， 在我國流行程度較為嚴重， 探討有效的預測方法對B肝的流行的預防控制具有重要意義。本文擬使用我國內地法定報告的 2005 年 －2011 年B肝月發病數時間序列為建立廣義神經網路模型，探討廣義回歸網路在B肝發病預測當中的實用價值。

實驗條件

以我國 2005 年 －2010 年這 6 年的月發病數據作為訓練樣本， 以 2011 年 12 個月的發病數作為驗證樣本， 分別建立 GRNN模型和傳統的 BP 神經網路預測模型(BPNN)， 進行預測對比實驗。模型的建立均在 Matlab 7.5 環境中實現。首先使用 Matlab 當中自帶的歸一化函式 mapminmax( )將發病數資料歸一化，歸一化的目的是取消數據間數量級的差別，避免因為輸入輸出數據數量級差別較大而造成網路預測誤差較大。神經網路時間序列模型一般選取時間序列的周期長度作為模型的輸入節點數。發病數資料的周期一般為一年。因此選取 12 作為本研究的輸入節點數， 即使用擬合或預測樣本的前12 個值作為當前訓練本。另外，本研究選取常用的單步預測法， 疊代預測驗證樣本的發病數， 因此輸出節點設為 1。光滑因子是 GRNN 中的重要參數，本研究分別設定其值為以 0.1 為步長 0.1 到 2.0 之間的值，使用 K- CV 法(本研究中取 K =3)訓練模型， 循環驗證， 選取最優模型， 確定最終網路結構。相對與GRNN， BPNN 模型當中設定的參數較多， 本研究僅使用 K- CV 法篩選 BPNN 的隱藏節點數， 隱藏節點分別設為 3 － 50， 循環驗證， 選取最有網路結構。隱含層神經元傳遞函式選擇正切 S 型函式，輸出層選擇線性傳遞函式， 學習函式選擇 Levenberg_Mar-quardt 的BP算法訓練函式， 學習速率設為 0.01， 目標精度為0. 001，網路反覆訓練 1000 次。

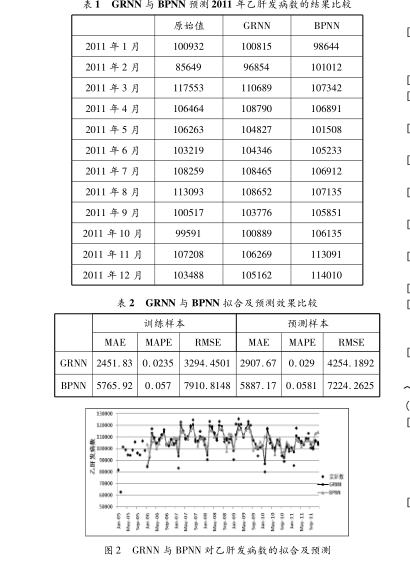
試驗結果與分析

經過篩選，最終確定 GRNN 模型的光滑因子值為 0.5，BPNN 的網路結構為 12 －5 －1， 兩種模型的預測結果和比較如表1和圖 所示，GRNN 與 BPNN 的預測值與真實值的MAPE 均控制在 10% 以內， 表明兩種方法均具有較好的預測效果，其中 GRNN 所得的訓練樣本及預測樣本的 MAE， MAPE 以及 MSE 均小於 BPNN， 因此認為， 在本次建模當中 GRNN 較BPNN 有較好的擬合效果及預測效果。BPNN 在本次建模當中預測效果相對欠佳。結果表明， GRNN 模型具有更好的擬合效果及預測效果，對於傳染病的預測具有良好的實用價值。相對於 BP 模型，GRNN模型的優點是模型結構簡單， 需要調整的參數少， 預測速度快，並且避免了繁瑣、 冗長的數學計算， 有較好的套用前景。