廣義哈納克原理

簡介

廣義哈納克原理是哈納克原理的推廣。

若{f_i|i∈I}是一族在區域D⊂Rⁿ內調和的函式組成的上定向集，即對i,j∈I，必有l∈I使得f_l≥f_i且f_l≥f_j，則必存在不減序列{f_i|i∈I₀⊂I}，使得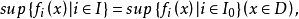

它或者恆為+∞，或者在D內調和。這個性質稱為廣義哈納克原理。

哈納克原理是斷言調和函式列的一致極限仍為調和函式的一個原理。

哈納克原理指出：設{fk}是在區域D內的調和函式列，若每個f_k在

上連續且{fk}在∂D上一致收斂，則{fk}在上一致收斂且極限函式f在D內調和；同時，在D的任意緊子集上，

都一致收斂於

其中m₁,m₂,...,m_n是任意取定的非負整數。

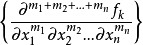
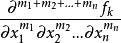
調和函式是在某區域中滿足拉普拉斯方程的函式。通常對函式本身還附加一些光滑性條件，例如有連續的一階和二階偏導數。當自變數為n個（從而區域是n維的）時，則稱它為n維調和函式。

對於高維的調和函式，也有與上述類似的最大、最小值原理，平均值公式以及相應的狄利克雷問題解的存在和惟一性定理。