基本介紹
- 中文名:廣義協調元
- 外文名:eneralized conforming element
- 提出者:龍馭球、辛克貴
- 提出時間:1987年
- 性質:一種基於勢能原理的位移元
- 優點:自由度少,精度高,程式簡便
簡介
理論基礎
領域開拓
主創人員
內容

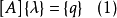
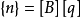




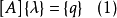
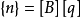


廣義協調元(eneralized conforming element),是由清華大學龍馭球與辛克貴在20世界80年代首創的,是有限元領域中一大突破。廣義協調元是一種基於勢能原理的位移元。其...
第2篇是有限元法進展初論,重點介紹廣義協調元;這是在協調元與非協調元之間另闢的新路,使收斂問題得到合理解決,單元構造方案可以靈活優選,學科內容得到充實更新;...
條有限元(1984),含可選參數變分原理(1986),廣義協調元(1987,辛克貴[1,2] ),四邊形面積坐標理論(1997),厚板層合板無閉鎖理性元(1998)和解析試函式有限元(...
辛克貴教授,博士生導師(Dr. XIN Ke-gui, Professor, Tsinghua University, Beijing),中國著名土木工程專家,傑出的力學家、教育家和橋樑專家,廣義協調元的重要創始人...
4、廣義協調元在橋樑分析中的套用.2008年獲天津市科技進步三等獎, 證書號:2008JB-3-068-R1,排名第一。4、項目主持人。道路工程貫通性裂縫分析及其維修關鍵施工...
[1] 第2篇是有限元法進展初論,重點介紹廣義協調元;這是在協調元與非協調元之間另闢的新路,使協調問題和收斂問題得到合理解決,單元構造方案可以靈活優選,學科...
第二節 薄板彎曲問題的有限元法---薄板三角形單元第三節 薄板彎曲問題的有限元法---矩形薄板單元第四節 剛性路面有限元分析第五節 用三角形薄板廣義協調元分析...
主要從事板殼理論、網架工程和有限元等方面研究。龍志飛人物成就 編輯 拓寬了有限元離散理論,創立了周協調和semiLoof型等廣義協調元新模式和新理論;利用廣義協調構造...
單元法外,還簡單介紹了廣義變分原理及其套用、加權餘量、廣義協調、半解析、樣條元和邊界單元法等基本知識,為適應部分專業研究生套用,還增加了非線性有限元的基礎...
