設m,n為正整數,p為素數,則C(下m+n上m)含p的冪次等於m+n在p進制下的進位次數。
基本介紹
- 中文名:庫默爾定理
- 外文名:Kummer Theorem
- 別稱:庫莫爾定理
- 套用學科:數論
簡要證明
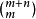

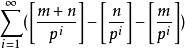
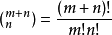


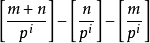
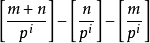
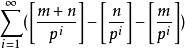
套用舉例










設m,n為正整數,p為素數,則C(下m+n上m)含p的冪次等於m+n在p進制下的進位次數。
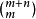

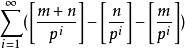
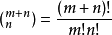


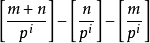
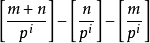
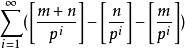










庫默爾定理編輯 鎖定 本詞條缺少概述圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!設m,n為正整數,p為素數,則C(下m+n上m)含p的冪次等於m+n在...
Herbrand-Ribet定理是某些數字域的類群的結果。 這是對恩斯特庫默爾定理的強化,即若且唯若p除以第n個伯努利數Bn的分子為n時,素數p除以單位第p個根的分圓場的...
庫默爾(Kummer,Ernst Eduard,1810.1.29-1893.5.14)德國數學家。生於索拉烏(Sorau,今波蘭的扎雷),卒於柏林。...
費馬大定理,又被稱為“費馬最後的定理”,由17世紀法國數學家皮耶·德·費瑪提出。他斷言當整數n >2時,關於x, y, z的方程 x^n + y^n = z^n 沒有正...
庫默爾早期研究超幾何級數,第一個計算單值群,晚期研究光學系統和彈道問題,發現著名的庫默爾曲面。他最重要的成就是在數論方面,特別是在試圖證明費馬大定理時引進了對...
庫默爾擴張是(Kummer extesion)是阿貝爾擴張的一種類型。因首先由E.E.庫默爾研究而得名。阿貝爾擴張是代數數論研究的主要對象。...
戴德金曾把伽羅瓦的結果解釋為關於域的自同構群的對偶定理。隨著20世紀20年代...廣義上的伽羅瓦理論還包括尺規作圖,諾特方程,循環擴張,庫默爾理論等內容。參考...
匯合型超幾何方程(confluent hypergeometric equation),亦稱庫默爾方程或者合流型超幾何方程,是常見的一種匯合型常微分方程。匯合型超幾何方程有兩個奇點,0和∞;...
毫無疑問,這裡的動機在於 K 的理想類群的p-撓部分已被恩斯特·庫默爾認出是他證明費馬大定理的主要障礙。岩澤健吉的創見在於他在一個新的意義上“跑到無窮大...
在數論中,正則素數的概念首先由恩斯特·庫默爾在1847年為了處理費馬最後定理而引入。它具有許多種等價的定義方式。...
匯合型超幾何函式(confluent hypergeometric function)亦稱庫默爾函式,是匯合型超幾何方程的基本解。而該方程則是常見的一種匯合型常微分方程。提出該方程函式的是...
