庫拉托夫斯基定理,即證明一個圖是平面圖的必要充分條件是 它不包含任何同胚於K5或K3,3的子圖。
基本介紹
- 中文名:庫拉托夫斯基定理
- 外文名:the Theorm of Kuratowski
- 提出者:Kuratowski
- 提出時間:1930年
- 套用學科:數學
- 適用領域範圍:幾何學
定理背景
判定方法
定理內容
作者
作者貢獻
- 庫拉托夫斯基閉包公理
- 塔斯基–庫拉托夫斯基算法
- 平面圖的庫拉托夫斯基定理
- 庫拉托夫斯基十四集問題
- 佐恩引理的證明
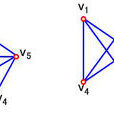
庫拉托夫斯基定理,即證明一個圖是平面圖的必要充分條件是 它不包含任何同胚於K5或K3,3的子圖。
庫拉托夫斯基定理,即證明一個圖是平面圖的必要充分條件是 它不包含任何同胚於K5或K3,3的子圖。...
這一定理是由庫拉托夫斯基(Kuratowski,K.)於1930年證明的,若可平面圖G不是任何同階其他可平面圖的子圖,則稱G為極大可平面圖,極大可平面圖所對應的平面圖的...
根據庫拉托夫斯基定理的擬陣版本,圖擬陣 的對偶擬陣也是圖擬陣,若且唯若M是平面圖的圖擬陣。這種情況下,M的對偶擬陣是G的對偶圖的擬陣。特定域F上可表示的向量...
波蘭數學家卡齊米日·庫拉托夫斯基提出的一類禁忌準則(指滿足某種條件的圖就一定無法具有某個性質)中,也包括了平面圖的情況。他提出的一個定理說明:...
12.2.1 平面圖定義12.2.2 庫拉托夫斯基定理12.3 對偶圖13.1 樹定義13.2 生成樹13.3 二叉樹13.4 生成樹的生成13.5 優美樹Ⅳ 數理邏輯14 命題邏輯...
§4 庫拉托夫斯基定理§5 可平面性算法§6 圖的交叉和厚度習題7第八章 圖的著色§1 邊色數§2 時間表問題§3 支配集與獨立集...
8.9.3非平面圖與庫拉托夫斯基定理211 8.10圖的著色212 8.10.1著色212 8.10.2對偶地圖與四色定理214 8.11圖在計算機存儲器中的表示215 8.11.1鄰接矩陣215 8....
庫拉托夫斯基定理/182第三部分 對應第六講 映射的套用 6.1 映射與一一對應/192 6.2 淘汰賽/195 6.3 鋸立方體/196 6.4 棋盤上的方格/197 6.5 對稱/199 6...
3.4.3 庫拉托夫斯基定理 3.4.4 正多面體 習題3.4 複習題 第4章 圖的簡單套用 4.1 圖的著色 習題4.1 4.2 最短路 4.2.1 狄克斯屈拉算法及其...
