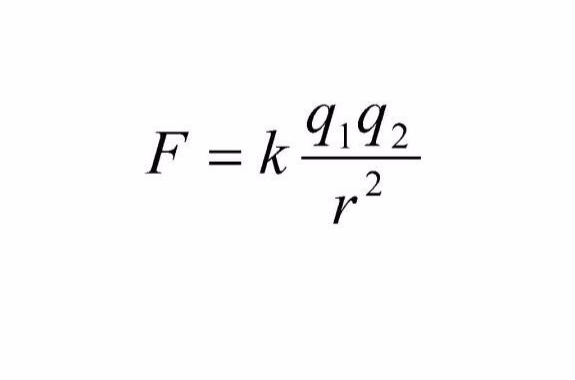定義
庫侖定律的
常見表述:真空中兩個靜止的點電荷之間的相互作用力,與它們的電荷量的乘積(
)成正比,與它們的距離的二次方(
)成反比,作用力的方向在它們的連線上,同名電荷相斥,異名電荷相吸。
庫侖定律的
數學表達式:
。其中r為兩者之間的距離;
為從q
1到q
2方向的矢徑;k為庫侖常數(靜電力常量)。當各個物理量都採用國際制單位時,
。用該公式計算時,不要把電荷的正負符號代入公式中,計算過程可用絕對值計算,可根據同名電荷相斥,異名電荷相吸來判斷力的方向。
適用範圍
適用條件
在庫侖定律的常見表述中,通常會有
真空和
靜止,是因為庫侖定律的實驗基礎——
扭秤實驗,為了排除其他因素的影響,是在亞真空中做的。另外,一般講
靜電現象時,常由真空中的情況開始,所以庫侖定律中有“真空”的說法。實際上,庫侖定律不僅適用於真空中,還適用於均勻介質中,也適用於靜止的點電荷之間。
庫侖定律還適用於均勻介質中。真空中的
庫侖力(d指的是兩電荷之間的距離),
k是一個普適常量,常引入
,
為真空中的
介電常數,實驗測得其大小
。根據
高斯定理,在均勻無限大介質中(介電常數
),兩個點電荷之間的相互作用力是真空中的
倍,即
,形式與真空的完全一樣。因此,庫侖定律不僅適用於真空,還適用於介質中。
庫侖定律適用於場源電荷靜止、受力電荷運動的情況,但不適用於運動電荷對靜止電荷的作用力。由於靜止的
場源電荷產生的
電場的空間分布情況是不隨時間變化的,所以,運動的電荷所受到的靜止場源電荷施加的電場力是遵循庫侖定律的;靜止的電荷所受到的由運動電荷激發的電場產生的電場力不遵守庫侖定律,因為運動電荷除了激發電場外,還要激發
磁場。此時,庫侖力需要修正為
電磁力。但實踐表明,只要電荷的相對運動速度遠小於
光速c,庫侖定律給出的結果與實際情形很接近。
庫侖定律只適用於點電荷之間。帶電體之間的距離比它們自身的大小大得多,以至形狀、大小及電荷的分布狀況對相互作用力的影響可以忽略,在研究它們的相互作用時,人們把它們抽象成一種理想的物理模型——點電荷,庫侖定律只適用於點電荷之間的受力。
局限性
庫侖定律沒有解決電荷間相互作用力是如何傳遞的,甚至按照庫侖定律的內容,庫侖力不需要接觸任何媒介,也不需要時間,而是直接從一個帶電體作用到另一個帶電體上的。即電荷之間的相互作用是一種“超距作用”,然而另一批物理學家認為這類力是“近距作用”,電力通過一種充滿在空間的彈性媒介——
以太來傳遞。
英國科學家
法拉第在研究電場時首先提出
場的觀點。他認為電荷會在其周圍空間激發
電場,處於電場中的其他電荷將受到力的作用,即電荷與電荷的相互作用時通過存在於它們之間的場來實現的。
現代科學已經證實,相互作用不是“超距”的,但“近距”觀點所假定的以太是不存在的,電荷之間存在相互作用力是通過電場來傳遞的,電荷之間相互作用的傳遞速度是
光速。
實驗
卡文迪許的同心球電荷分布實驗,比庫侖的
扭秤實驗精確且早幾十年,但是卡文迪許並沒有發表自己的著作。直到1871年麥克斯韋主持劍橋大學的卡文迪許實驗室後,卡文迪許的手稿才轉到了麥克斯韋手中,麥克斯韋親自動手重複了卡文迪許的許多實驗,手稿經麥克斯韋整理後出版,他的工作才為世人所知。
1769年,英國蘇格蘭人羅賓遜,設計了一個槓桿裝置,他把實驗結果用公式 表述出來,即電力 F與距離 r的 n次方成反比。先假設指數 n不是準確為2,而是 ,得到指數偏差 。 | 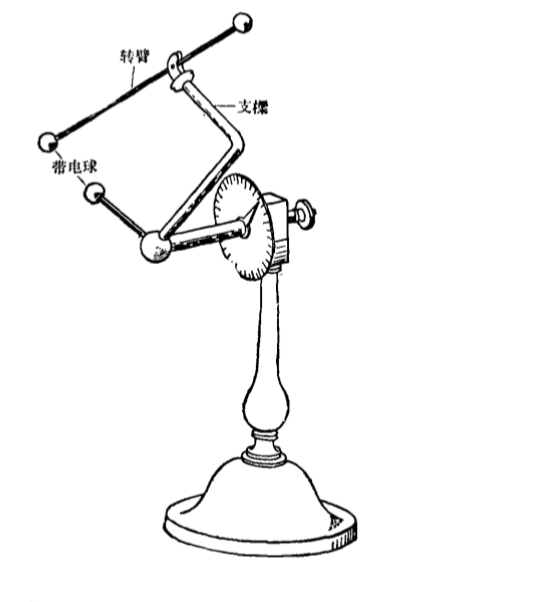 羅賓遜的實驗裝置 羅賓遜的實驗裝置 |
1784年至1785年間,法國物理學家查爾斯· 庫侖通過扭秤實驗驗證了這一定律。扭秤的結構如右圖所示:在細金屬絲下懸掛一根秤桿,它的一端有一小球A,另一端有平衡體P,在A旁還置有另一與它一樣大小的固定小球B。為了研究帶電體之間的作用力,先使A、B各帶一定的電荷,這時 秤桿會因A端受力而偏轉。轉動懸絲上端的懸鈕,使小球回到原來位置。這時懸絲的扭 力矩等於施於小球A上電力的力矩。如果懸絲的扭力矩與扭轉角度之間的關係已事先校準、標定,則由旋鈕上指針轉過的角度讀數和已知的秤桿長度,可以得知在此距離下A、B之間的作用力,並且通過懸絲扭轉的角度可以比較力的大小。 | |
1773年,卡文迪許用兩個同心金屬球殼做實驗,如右圖,外球殼由兩個半圓裝配而成,兩半球合起來正好把內球封在其中。通過一根導線將內外球連在一起,外球殼帶點後,取走導線,打開外殼,用木髓球驗電器試驗有沒有帶電,結果發現木髓球驗電器沒有指示,內球不帶電荷。根據這個實驗,卡文迪許確定指數偏差 ,比羅賓遜1769年得出的0.06更精確。 1873年,麥克斯韋和麥克阿利斯特改進了 卡文迪許的這個實驗。麥克斯韋親自設計實驗裝置和實驗方法,並推算了實驗的處理公式。 他們將 F表示為 ,其中 q不超過 。這個實驗做得十分精確,以致直到1936年未曾有人超過他們。 | 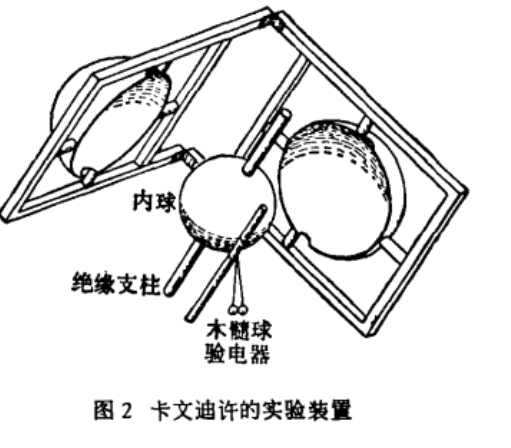 卡文迪許的實驗裝置 卡文迪許的實驗裝置 |
1936年,美國沃塞斯特工學院的Plimpton和Lawton,在新的基礎上驗證了庫侖定律,他們運用新的測量手段,改進了卡文迪許和麥克斯韋的零值法,消除和避免了試驗中幾項主要誤差,從而大大地提高了測量精度,試驗線路和裝置如右圖所示。他們用這套裝置進行了多次試驗,不同的實驗者都確認電流計除了由於熱運動造成的1微伏指示外沒有其他振動,他們用麥克斯韋對出的公式進行計算,得到 | 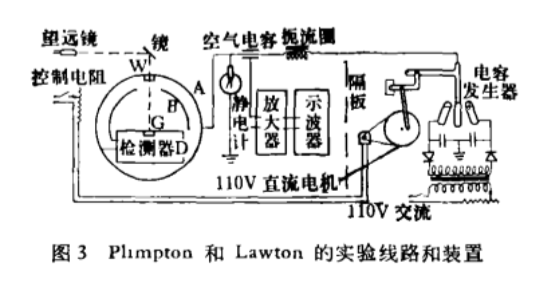 Plimpton和Lawton的實驗裝置 Plimpton和Lawton的實驗裝置 |
1971年,美國Wesleyan大學的Edwin R.Williams,James E.Faller及Henry A.Hill用現代測試手段,將平方反比定律的指數偏差又延伸了好幾個數量級。在此之前已有好幾起實驗結果,不斷地刷新紀錄。Williams等人採用高頻高壓信號、鎖定放大器和光學纖維傳輸來保證實驗條件,但基本方法和設計思想跟卡文迪許和麥克斯韋是一脈相承的。 右圖是簡單示意圖,他們用五個同心金屬殼,而不是兩個,採用十二面體形,而不是球形。峰值為10千伏的4兆赫高頻高壓信號加在最外面兩層金屬殼上,檢測器接到最裡面的兩層,檢驗是否接收到信號。 他們根據麥克斯韋的公式,得到的平方反比定律的指數偏差 | 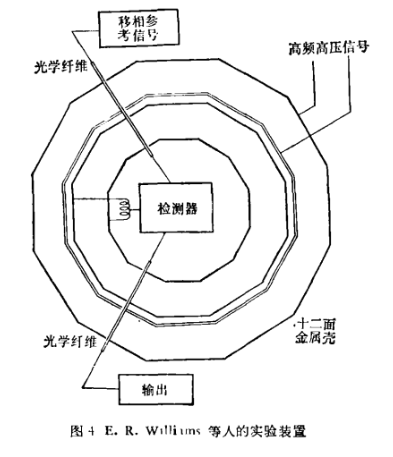 現代實驗裝置 現代實驗裝置 |
評價
庫倫定律由法國物理學家
庫侖於1785年在《電力定律》一論文中提出。庫侖定律是電學發展史上的第一個定量規律,是
電磁學和
電磁場理論的基本定律之一。
庫侖定律不僅是
電磁學的基本定律,也是物理學的基本
定律之一。庫侖定律闡明了帶電體相互作用的規律,決定了
靜電場的性質,也為整個電磁學奠定了基礎。庫侖的工作對法國物理學家的影響還可以從稍後的
拉普拉斯的物理學簡略綱領得到證實。這個物理學
簡略綱領最基本的出發點是把一切物理現象都簡化為
粒子間
吸引力和排斥力的現象,電或磁的運動是荷電粒子或荷磁粒子之間的吸引力和排斥力產生的
效應。這種簡化便於把分析數學的方法運用於物理學。
電量的單位是為了紀念庫侖而以他的名字命名的。(符號是Q,單位庫倫,符號C)




















 羅賓遜的實驗裝置
羅賓遜的實驗裝置



 卡文迪許的實驗裝置
卡文迪許的實驗裝置
 Plimpton和Lawton的實驗裝置
Plimpton和Lawton的實驗裝置
 現代實驗裝置
現代實驗裝置