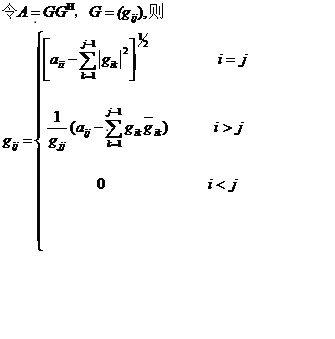Cholesky 分解是把一個對稱正定的矩陣表示成一個下三角矩陣L和其轉置的乘積的分解。它要求矩陣的所有特徵值必須大於零,故分解的下三角的對角元也是大於零的。Cholesky分解法又稱平方根法,是當A為實對稱正定矩陣時,LU三角分解法的變形。
基本介紹
- 中文名:cholesky分解
- 又稱:平方根法
- 相關:當A為實對稱正定矩陣時
- 變形:LU三角分解法的變形
重要性質,證明方式,分解定義,遞推公式,
重要性質
1.若A對稱正定,則 亦對稱正定,且
亦對稱正定,且 >0;
>0;


2.A的順序主子陣 亦對稱正定;
亦對稱正定;

3.A的特徵值λi>0;
4.A的全部順序主子式det( )>0。(A能夠作Cholesky分解的充要條件)
)>0。(A能夠作Cholesky分解的充要條件)

證明方式
設A= >0,則A的所有順序主子式為正
>0,則A的所有順序主子式為正


矩陣A存在Doolittle分解:A=L1U
易證 =
= ,i=1,2,...,n
,i=1,2,...,n


其中di(i=1,...,n)為U的主對角元素,且有
di>0,i=1,2,...,n
記D=diag(d1,d2,...,dn)
A^T=A,(L1U)^T=L1U,U^T(L1)^T=L1U
(D^(-1)U)^TD(L1)^T=L1D(D^(-1)U)
(L1)^T(D^(-1)U)^(-1)=D^(-1)(U^(-1)D)^TL1D
D^(-1)U=(L1)^T,A=L1D(L1)^T,A=L1D^(1/2)D^(1/2)(L1)^T
A=(L1D^(1/2))(L1D^(1/2))^T
即
A=LL^T
分解定義
如果矩陣A為n階對稱正定矩陣,則存在一個對角元素為正數的下三角實矩陣L,使得:當限定L的對角元素為正時,這種分解是唯一的,稱為Cholesky分解。在Matlab中,Cholesky分解由函式chol實現,該函式要求輸入的矩陣是正定的。
遞推公式