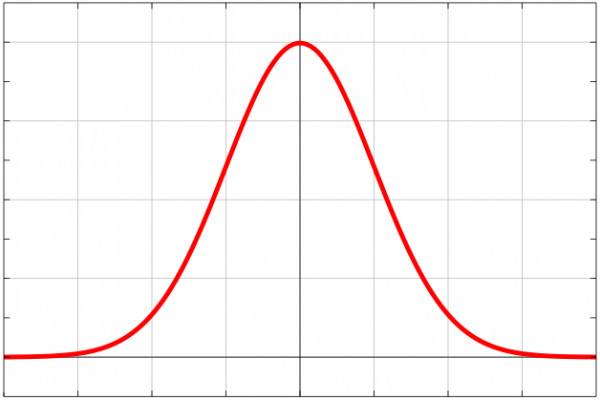
常態分布曲線是一種對稱的鐘形曲線,具有均數等於0,標準差等於1的特點,從而使標準分數在實際運用時非常有用。
基本介紹
- 中文名:常態分布曲線
- 外文名:The normal distribution curve
- 性質:數學術語
- 分類:鐘形曲線
- 學科:數學、統計學
背景
定義
套用
實現過程
1.在A1輸入公式

2.在B1輸入公式

3.下拉複製上面的兩個公式分別到
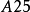
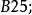
常態分布曲線是一種對稱的鐘形曲線,具有均數等於0,標準差等於1的特點,從而使標準分數在實際運用時非常有用。


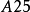
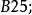
常態分布曲線是一種對稱的鐘形曲線,具有均數等於0,標準差等於1的特點,從而使標準分數在實際運用時非常有用。...
常態分配曲線反映了隨機變數的分布規律。理論上的常態分配曲線是一條中間高,兩端逐漸下降且完全對稱的鐘形曲線。...
分布曲線是以變數值為橫坐標,以累積頻率[機率]為縱坐標的曲線圖,即機率分布函式的圖形。例如正態曲線等。...
常態分配(Normal distribution),也稱“常態分布”,又名高斯分布(Gaussian distribution),最早由A.棣莫弗在求二項分布的漸近公式中得到。C.F.高斯在研究測量誤差時...
即常態分配曲線normaldistribution,一種機率分布。常態分配是具有兩個參數μ和σ2的連續。 型隨機變數的分布,第一參數μ是服從常態分配的隨機變數的均值,第二個...
3、均勻變動性:成績分布曲線由平均成績所在處開始,分別向左右兩側逐漸均勻下降成績常態分配作用 編輯 在進行選拔性測驗時(如中考、高考),由於是一種難度測驗,它...
標準常態分配又稱為u分布,是以0為均數、以1為標準差的常態分配,記為N(0,1)。標準常態分配曲線下面積分布規律是:在-1.96~+1.96範圍內曲線下的面積等於0....
當均值和標準差確定時,一個常態分配曲線就確定了 [1] 。均值μ是常態分配曲線的位置參數,不同的正態曲線,當標準差σ相同時其曲線形態相同,只是曲線中心的位置...
1、在實際遇到的許多隨機現象都服從或近似服從常態分配 [1] 。當樣本頻率分布直方圖就無限接近於一條總體密度曲線,總體密度曲線較科學地反映了總體分布。但總體密度...
偏態分布是與“常態分配”相對,分布曲線左右不對稱的數據次數分布,是連續隨機變數機率分布的一種。可以通過峰度和偏度的計算,衡量偏態的程度。可分為正偏態和負...
鐘型曲線又稱正態曲線,它是一根兩端低中間高的曲線。它首先被數學家用來描述科學觀察中量度與誤差兩者的分布。比利時天文學家奎斯勒首先提出大多數人的特性均趨向...
利用這張常態分配圖,你將很容易區分出業績排在前面的20%的員工(A類)、中間的...B級員工是中間的70%;C級員工約10%,奇異以常態分配的鐘形活力曲線(Vitality ...
1.實際工作中,正態曲線下橫軸上一定區間的面積反映該區間的例數占總例數的百分比,或變數值落在該區間的機率(機率分布)。不同 範圍內正態曲線下的面積可用公式3...
越來越大),分布曲線也越來越低闊(因為方差 越來越大)。3)不同的自由度決定不同的卡方分布,自由度越小,分布越偏斜。4) 若 互相獨立,則: 服從 分布,自由度...
