如果向量格X同時是巴拿赫空間,且序和範數之間有關係:|xl≤ly|推出‖x‖≤‖y‖(x,y∈X),則稱X為格序巴拿赫空間或巴拿赫格。
基本介紹
- 中文名:巴拿赫格
- 外文名:Banach lattice
- 適用範圍:數理科學
簡介,實例,性質,收斂,
簡介
巴拿赫格是兼有巴拿赫空間特性的向量格。
如果向量格X同時是巴拿赫空間,且序和範數之間有關係:|xl≤ly|推出‖x‖≤‖y‖(x,y∈X),則稱X為格序巴拿赫空間或巴拿赫格。
實例
例如,數列空間c,lp(p≥1)以及函式空間C[a,b],Lp[a,b](p≥1)等,按自然的序關係(即這些空間的元如在每個點或坐標處的值≥0時是正元)形成巴拿赫格。
性質
在巴拿赫格中,當
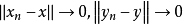
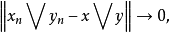
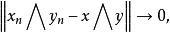
收斂
關於巴拿赫格中序收斂和範數收斂的強弱的比較,儘管在不同具體空間結論不一樣。
然而‖xn-x‖→0同{xn}相對一致∗收斂於x(即對{xn}的任何子列{xn(m)},存在此子列的子列{xn(m(l))}和某y∈X,使得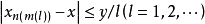 是等價的。
是等價的。
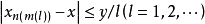
又,序意義下的有界集必是範數意義下的有界集,但其逆一般不真。
