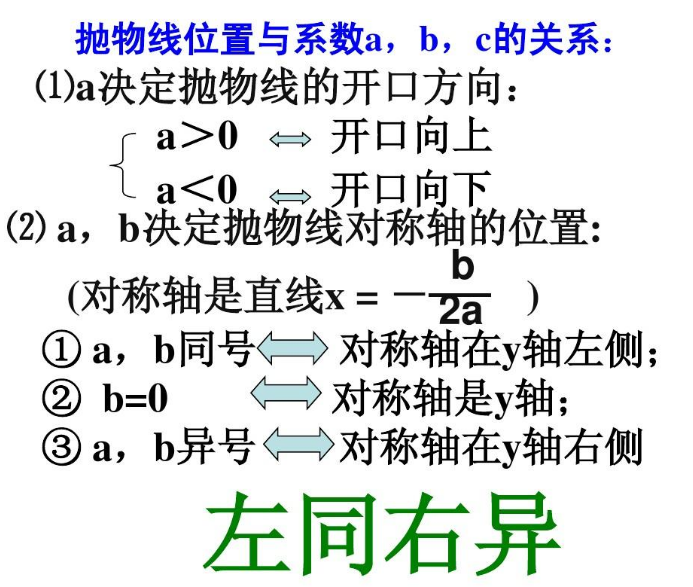
基本介紹
- 中文名：左同右異
- 適用領域：二次函式
- 套用學科：數學
- 性質：簡單記憶口訣
- 作用：決定對稱軸位置
主要公式,主要數據,
主要公式
在蒸蘭霉二次函式中，決定對稱軸位置的因素的簡單記憶口訣。
設二次函式
：
當a與b同號時（即a,b＞0），對稱軸在y軸左； 因為若對稱軸在左邊則對稱軸小於0，也就是
<0,所以
>0，所以a、b要同號 。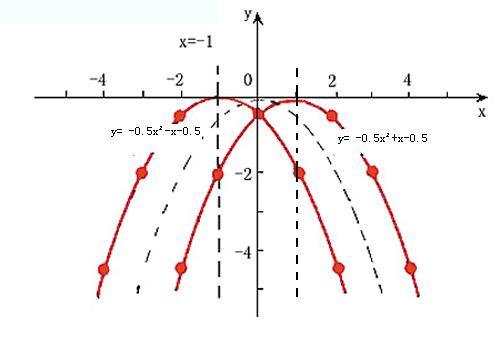
二次函式
當a與b異號時（即a,b<0），對稱軸在y軸右。頸戲妹試因為對稱軸在右邊則對稱軸要大於0，也就是 >0, 所以＜0，所以a、b要異號陵頸灑 。
主要數據
可簡單記憶為左同右異，即當a與b同號時（即ab＞0），對稱軸在y軸左；當a與b異號時 （即ab＜0 ），對稱軸在y軸右。
例題：
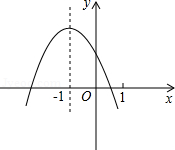
圖1 二次函式
（2012·威海）已知二次函式（a≠0）的圖象如圖1所示，下列結論錯誤的是（ ）
A． | abc>0 | B． | 3a>2b |
C． | m（am+b）≤a﹣b（m為任意實數） | D． | 4a﹣2b+c<0 |
考點： | 二次函式圖象與係數的關係． |
分析： | 根據函式圖殃陵象可得各係數的關係：a≠0，根據對稱軸x= |
解答： | 解：A．由函式圖象可得各系匪提套愉數的關係：a≠0，對稱軸x= 故abc>0，故此選項正確，但不符合題意； B．∵x= ∴b=2a， ∴2b=4a， ∵a<0，b<0， ∴3a>2b，故此選項正確，但不符合題意； C．∵b=2a，代入m（am+b）﹣（a﹣b）得： ∴m（am+2a）﹣（a﹣2a）， =am2+2am+a， =a（m+1）2， ∵a<0， ∴a（m+1）2≤0， ∴m（am+b）﹣（a﹣b）≤0， 即m（am+b）≤a﹣b，故此選項正確，但不符合題意； D．當x=﹣2代入y=ax2+bx+c，得出y=4a﹣2b+c， 利用圖象與x軸蘭廈漿交點右側小於1，則得出圖象與坐標軸左側交點一定小於﹣2， 故y=4a﹣2b+c>0，故此選項錯誤，符合題意； 故選：D． |
點評： | 此題主要考查了二次函式圖象與係數的關係，同學們應注意，二次函式y=ax2+bx+c（a≠0）的圖象，當ab>0，對稱軸在y軸左；當a與b異號時（即ab<0），對稱軸在y軸右，以及利用對稱軸得出a，b的關係是解題關鍵． |
