基本介紹
- 中文名:嵌入下推自動機
- 縮寫:EPDA
- 性質:計算模型
- 領域:計算機
歷史和套用,理論,計算模型,上下文有關文法,
歷史和套用
EPDA 最初由 K. Vijay-Shanker 在他 1998 年的博士論文中描述。它們已經被套用於更完整的描述適度上下文有關文法類,並向喬姆斯基層級擴展和精細了這個文法類。各種子文法,比如線性附標文法可以從而定義。它們還在自然語言處理中扮演重要角色。
理論
首先重申 EPDA 是有一組其自身可以通過“嵌入棧”來訪問的棧的有限狀態機,每個棧包含“棧字母表” 的元素,並且我們通過
的元素,並且我們通過 定義一個棧的元素,這裡的星號是字母表的Kleene閉包。
定義一個棧的元素,這裡的星號是字母表的Kleene閉包。


每個棧都可以依據它的元素來定義,所以我們使用雙劍符號來指示在自動機中的第 個棧: ,這裡的
,這裡的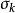 將是在棧中的下一個可訪問的符號。
將是在棧中的下一個可訪問的符號。 個棧的“嵌入棧”因此可以指示為
個棧的“嵌入棧”因此可以指示為 。
。

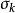


我們定義 EPDA 為七元組:

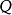


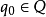





所以轉移函式選取一個狀態,輸入字元串的下一個符號,和當前棧的頂符號;並生成下一個狀態,在“嵌入棧”上要壓入和彈出的那些棧,當前棧的壓入和彈出,和要在下一個轉移中被當作當前棧的棧。更加概念的說,“嵌入棧”是被壓入和彈出的,當前棧被隨意的壓回到“嵌入棧”,而你希望的任何其他棧將被壓入它的頂部,帶有最後的棧是在下一個重複中所讀取的。所以,這些棧被同時壓入當前棧的上面和下面。
一個給定的格局被定義為

這裡的 是當前狀態,
是當前狀態, 是在“嵌入棧”中的棧,帶有
是在“嵌入棧”中的棧,帶有 是當前棧,而對於輸入字元串
是當前棧,而對於輸入字元串  是已經被機器處理的那部分字元串,而
是已經被機器處理的那部分字元串,而  是要處理的那部分,帶有它的頭部是當前所讀的符號。注意空串
是要處理的那部分,帶有它的頭部是當前所讀的符號。注意空串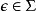 被隱含的定義為終止符號,如果機器處於最終狀態此時讀到空串,則整個輸入字元串被“接受”,如果不是則“拒絕”。這種“接受”了的字元串是如下語言的元素
被隱含的定義為終止符號,如果機器處於最終狀態此時讀到空串,則整個輸入字元串被“接受”,如果不是則“拒絕”。這種“接受”了的字元串是如下語言的元素





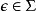
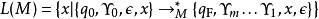
計算模型
計算模型(computational model)是計算科學中的一個數學模型,它使用大量的計算資源來用計算機模擬研究一個複雜系統的行為。被研究的系統通常是一個複雜的非線性系統,這種系統不易取得簡單、直觀的解析解。相比於推導數學分析來解決問題,它是通過在計算機中調整系統參數並研究實驗結果的差異來完成模型。模型的操作理論可以從這些實驗來推斷/推導。
