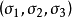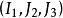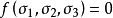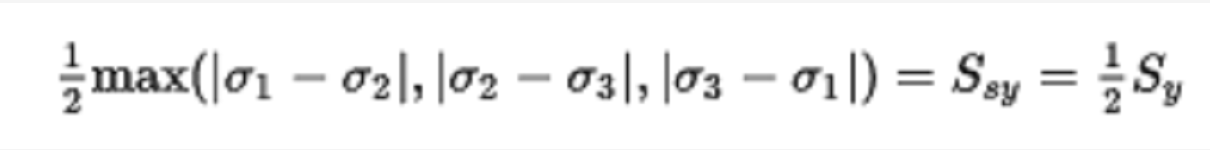屈服面是應力六維空間中的五維表面。屈服面通常是凸的，屈服面內部的應力狀態是彈性的。當應力狀態位於表面上時，材料被稱為已經達到其屈服點，並且材料據說已經變成塑性。材料的進一步變形會導致應力狀態保持在屈服面上，即使表面的形狀和尺寸隨著塑性變形的發展而發生變化。這是因為位於屈服面之外的應力狀態在速率無關塑性方面是不允許的，儘管不是在某些粘塑性模型中。
基本介紹
- 中文名：屈服面
- 外文名：Yield surface
- 學科：材料力學
- 原因：物體受荷載作用
- 狀態：彈性狀態過渡到塑性狀態
- 相關名詞：屈服應力
概述,屈服面的例子,特雷斯卡產量表面,等效應力屈服面,Drucker-Prager屈服面,威拉姆沃恩克屈服面,
概述
屈服面是應力六維空間中的五維表面。屈服面通常是凸的，屈服面內部的應力狀態是彈性的。當應力狀態位於表面上時，材料被稱為已經達到其屈服點，並且材料據說已經變成塑膠。材料的進一步變形會導致應力狀態保持在屈服面上，即使表面的形狀和尺寸隨著塑性變形的發展而發生變化。這是因為位於屈服面之外的應力狀態在速率無關塑性方面是不允許的，儘管不是在某些粘塑性模型中。
屈服面通常用三維主應力空間
，由應力不變數
跨越的二維或三維空間或者是三維海威特高壓應力空間。 因此，我們可以在形式中寫出屈服表面的方程（即屈服函式）：
其中因變數是主要的應力。
其中I1是柯西應力的第一個主不變數，J2，J3是偏差部分的第二和第三主不變數的柯西應力。
一個應力狀態可以用6 維應力空間中點代表。 一般的彈塑性理論認為， 在應力空間可以劃出一定的彈性區， 區內每一點代表一種彈性應力狀態，限制彈性區的表面稱為屈服面。加荷時屈服面被突破， 整個應變張量的6個分量都將發生塑性應變，同時形成新的屈服面。但是把這種單一屈服面的理論搬用於土力學中， 結果不能認為是滿意的。為了更好地說明上的彈塑性變形性質，不少人提出兩個屈服面的理論。
屈服面的例子
工程中有幾種不同的屈服面，最流行的屈服面如下。
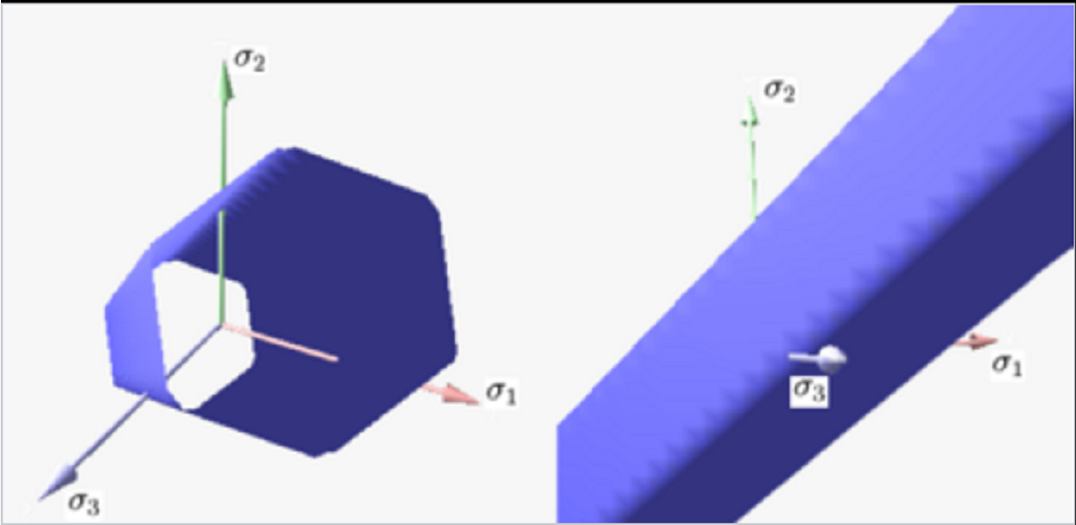
特雷斯卡產量表面
特雷斯卡產量標準被認為是亨利特雷斯卡的工作。也稱為最大剪下應力理論（MSST）。 在主應力方面，特雷斯卡標準表示為
其中Sxy是剪下中的屈服強度，Sy是拉伸屈服強度。
下面圖顯示了主應力三維空間中的Tresca-Guest屈服面。 它是六面稜鏡，具有無限長。 這意味著當所有三個主應力大致相當（靜水壓力）時，材料保持彈性，無論壓縮或拉伸多少。 然而，當主應力之一變得比其他主應力變小（或更大）時，材料受到剪下。 在這種情況下，如果剪下應力達到屈服極限，則材料進入塑性區域。
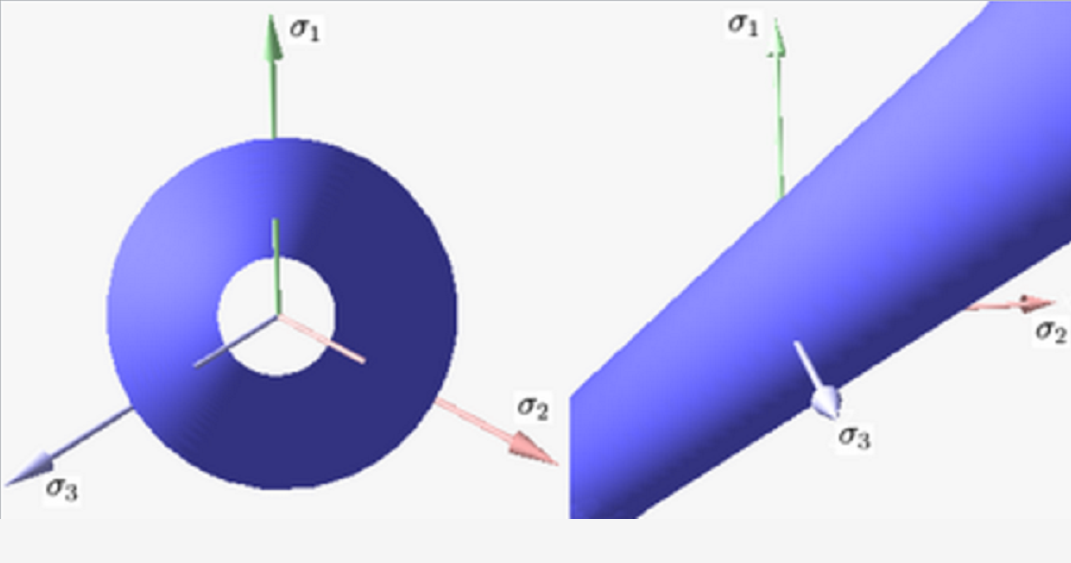
等效應力屈服面
等效應力屈服準則在主要應力中表示為
其中Sy是單軸張力的屈服強度。
下圖顯示了主應力三維空間中的等效應力屈服面。 它是一個無限長的圓柱體，其軸線與三個主應力相等傾斜。
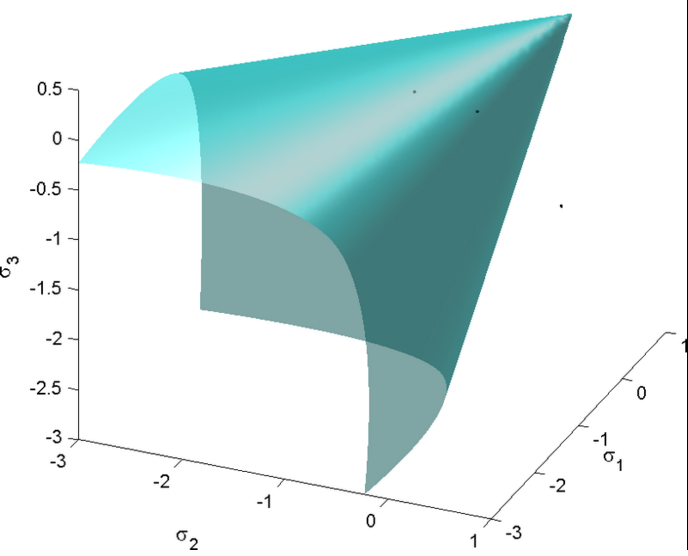
Drucker-Prager屈服面
Drucker-Prager屈服準則類似於等效應力屈服準則，其規定用於處理具有不同拉伸和壓縮屈服強度的材料。 該標準最常用於混凝土，其中正應力和剪下應力都可以確定失效。 Drucker-Prager屈服準則可以表示為
和Syc，Syt分別是壓縮和張力的單軸屈服應力。如果Syc=Syt，則公式減少為von Mises方程。
下圖顯示了Drucker-Prager屈服面在主應力三維空間中的表面。它是一個常規的錐體。橢圓彈性域是σ1，σ2的平面上的錐體的橫截面。可以選擇它在不同數量頂點的莫爾 - 庫侖屈服面相交。一個選擇是在σ1=-σ2行的任一側的三個頂點處與Mohr-Coulomb屈服面相交，但通常按慣例選擇是壓縮機制中的那些。另一個選擇是在兩個軸上的四個頂點（單軸擬合）或對角線上的兩個頂點σ1=σ2與Mohr-Coulomb屈服面相交（雙軸擬合）。Drucker-Prager屈服準則也通常以材料內聚力和摩擦角表示。
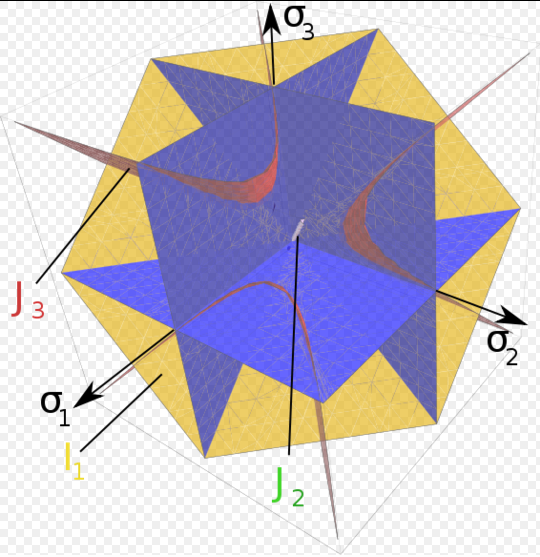
威拉姆沃恩克屈服面
威拉姆沃恩克屈服準則是Mohr-Coulomb屈服準則的三參數平滑版本，其形式與Drucker-Prager和Bresler-Pister產量標準相似。
產量準則具有功能形式
當沿其軸線觀察時，表面的橫截面是平滑的三角形（不同於Mohr-Coulumb）。 Willam-Warnke屈服面是凸的，並且在其表面的每個點上都具有獨特且明確的第一和第二導數。 因此，威拉姆 - 瓦恩克（Willam-Warnke）模型在計算上非常強大，已被用於各種粘性摩擦材料。
