局部李普希茨函式(locally Lipschitz function)一種局部一致的連續函式。
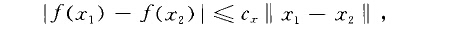
局部李普希茨函式(locally Lipschitz function)一種局部一致的連續函式。
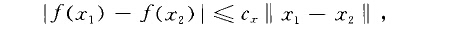
局部李普希茨函式(locally Lipschitz function)一種局部一致的連續函式。...... 局部李普希茨函式(locally Lipschitz function)[1] 一種局部一致的連續函式。...
李普希茨條件(Lipschitz condition)亦稱赫爾德條件,限制函式增量變化大小的一種不等式形式的條件,若f是區間I上的函式,存在正的常數L和α(0<α≤1),使得只要x1,x...
李普希茨(Lipschitz,Rudolf Otto Sigismund 1832.5.14—1903.10.7)是德國數學家。生於柯尼斯堡,卒于波恩。1847年入柯尼斯堡大學,不久轉入柏林大學跟隨狄利克雷...
則稱f 為雙李普希茨(bi-Lipschitz)的。利普希茨連續定理 編輯 (此定理又稱...所有C1函式都是局部利普希茨的,因為局部緊緻空間的連續函式必定有界。...
若且唯若處處可微函式f的一次導函式有界,f符利普希茨條件。這是中值定理的結果。所有 函式都是局部利普希茨的,因為局部緊緻空間的連續函式必定有界。 [2] ...
非光滑分析就致力於更一般的廣義微分法,來處理非光滑函式的極值問題。這方面最成功的是克拉克(Clarke,F.H.)對局部李普希茨函式提出的廣義梯度理論,他在1983年出版...
上定義且連續並滿足局部李普希茨條件,同時設 ,因此,對任何初始值 ,存在(1)的惟一的解 滿足 。由李亞普諾夫第二方法知道,如果存在一個定正函式 ,它關於(1)的...
這裡f:G→Rn是連續的且滿足局部李普希茨條件,其中G⊂Rn為開集,稱純量函式V是G上的李亞普諾夫函式。如果V在G的閉包Ḡ上連續,在G內連續可微,且 令 設M...
廣義梯度(generalized gradient)是梯度或導數概念的一種推廣,這是克拉克(Clarke,F.H.)對於局部李普希茨函式類提出的概念,由此形成的理論目前已成為非光滑分析中最...
