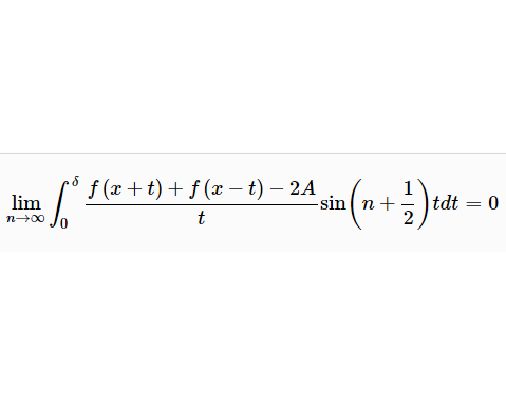局部化原理

局部化原理(localized principle)是傅立葉部分和收斂的一個特徵，可積函式f的傅立葉部分和S_n(f，x)在一點x處的收斂性態只依賴於f在該點附近的性狀，這一原理稱為黎曼局部化原理。確切地說，若可積函式f在x₀的一個鄰域(x₀-δ，x₀+δ)(δ>0可任意小)上恆為零，則：lim_n→∞S_n(f，x₀)=0=f(x₀)，值得注意的是，對於多變元函式的傅立葉級數，局部化的問題是相當複雜的。

基本介紹

• 中文名：局部化原理
• 外文名：localized principle
• 所屬學科：數學
• 所屬問題：調和分析(一元傅立葉分析)
• 相關概念：傅立葉級數、收斂性定理等
• 定義：傅立葉部分和收斂的一個特徵

基本介紹

(黎曼局部化原理)設 是在區間 上按一段連續的以 為周期的周期函式，A是一常數，則從 導出的傅立葉級數

在定點x處收斂於A的充要條件是： 對於任意 都有

注意(2)式（和下面的(3)）式中的積分是在 上取的，因此只涉及到 在 這一區間上的值，和 在這一區間以外的值無關。而 又是任意的，因此黎曼局部化原理(和下面命題1)說明從 導出的傅立葉級數(1)在定點x處是否收斂(於某常數A)，只和 在點x附近的性質有關，這就是黎曼局部化原理(和下面命題1)稱為局部化原理的原因。

相關命題與定理

如果 是在 上按段連續的以 為周期的函式，A是一常數，則從 導出的傅立葉級數(1)在x點收斂於A的充要條件是：對子任意 都有

為了把（3）式寫成更便於套用的形式，注意

所以對於固定的x，

是 的在 上按段連續的函式，於是由黎曼引理，

從而，(3)式成立與

成立是等價的，於是命題1可改進為黎曼局部化原理。

收斂性定理

根據黎曼局部化原理，立即可得下述收斂性定理：

如果 是在 上按段光滑的以 為周期的周期函式，則從 導出的傅立葉級數(1)是處處收斂的，其和是 即有

注意，如果 在點x 處連續，則 因此當 滿足收斂性定理的條件時，從它導出的傳里葉級數必在 的一切連續點處收斂於 。