基本介紹
- 中文名：對角線悖論
- 外文名：diagonal Paradox
- 所屬學科：數學（數理邏輯）
- 提出者：湯姆遜
- 相關概念：康托爾對角線方法
基本介紹,對角線方法與對角線悖論,
基本介紹
湯姆森指出：羅素悖論、格瑞林悖論和里夏爾悖論都是建立在康托爾對角線方法之上。現代一些邏輯學家幾乎把所有邏輯悖論(集合論的和語義學的)都稱為對角線悖論，包括著名的哥德爾不完全性定理。
“對角線證法"是康托爾在無窮集合的研究中得出的。1873年康托爾在他與戴德金的一次通信中提出實數集是否能和自然數集構成一一對應的問題。康托爾於1874年的文章給出了一個複雜的證明之後，他又給出了一個不依賴於無理數的技術性的證明，這就是熟知的優美而深刻的“對角線證法"，這是用完全直觀的無窮階方陣的“對角線”構造了一個不包含在某個假設為已知的集合的元素，也就是在一個特定的系統中構造一個“自我否定”，這正是這一方法的實質。在悖論各種證明中，“對角線證法’’得到了離開直觀的發揮和推廣。
“對角線證法”不斷地反覆出現在遞歸函式論、計算機科學中。還出現在哥德爾第一不完全性定理的證明和A.塔斯基關於真理的論證中。
湯姆遜在《論一些悖論》一文中對康托爾的“對角線證法"進行了更一般抽象的表示。安德遜認為此文是關於“對角線證法”論述得最清楚簡要的文章。
對角線方法與對角線悖論
對角線方法是一種重要的反證法，為康托爾(G.F.P.Cantor)於1874年所創造，它第一次用來證明實數集是不可數的，為了證明R是不可數的，只要證明[0，1]R不可數，現用反證法，設[0，1]可數，則可設[0，1]={a1，a2，…，an，…}.由於an∈[0，1]，故可用無窮十進制小數表示，並將這些數依次列出：
a1=0.a11a12a13… a1n…
a2=0.a21a22a23… a2n…
a3=0.a31a32a33… a3n…
…………………………
an=0.an1an2an3… ann…
…………………………
現在定義一數b=0.b1b2… bn…，其中
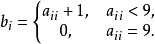
則顯然b∈[0，1]。但b≠ai，i=1，2，…，n，…這樣就與[0，1]可數相矛盾，即證明了[0，1]不可數，從而R不可數.這種用完全直觀的無窮階方陣的對角線構造出一個不包含在某個集合的元素，也就是在特定的系統中構造一個自我否定，正是在這一方法精神實質的指導下，對角線方法得到了脫離直觀的發揮和推廣，康托爾用對角線方法證明了他著名的定理：對任意集合A，|P(A)|>|A|，現在，對角線方法反覆地出現在遞歸函式論、計算機科學中，還出現在哥德爾(K.Gödel)的第一不完全性定理的證明和塔爾斯基(A.Tarski)關於真理的論證中，湯姆森(Thomson，W.(L.K.))在《論一些悖論》一文中對對角線方法進行了更一般的抽象表示：設S是一集合，P是一個二元謂詞，對每個b∈S定義一個一元謂詞：
Pb(a)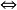
P(a，b) (∀a，b∈S)，
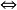
則對角線引理即為：設P為二元謂詞，定義一個一元謂詞Q為：
Q(a)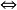
P(a，a) (∀a∈S)，
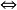
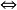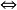
則Q(a)與所有的Pb(a)不同，∀b∈S.可以看出對角線證法的關鍵在於構成一個自我否定的例外，作為前提的外部關係：Pb(a)P(a，b)沒有矛盾，而當把二元關係變為否定的內部的一元關係(P(b，b))的特殊情形時，出現了矛盾，在前提中並沒有錯誤，而是在作為外部關係的理論形式邏輯推理中出現了內部的自我否定P(b，b)P(b，b)。
