基本介紹
- 中文名:對偶正多面體
- 外文名:dual regular polyhedron
- 別名:共軛正多面體
- 簡介:滿足特定條件的兩個正多面體
基本介紹





相關詞條
- 對偶正多面體
對偶正多面體(dual regular polyhedron)亦稱共軛正多面體,是滿足特定條件的兩個正多面體。如果兩個正多面體的棱數相等,並且其中一個的頂點數恰好等於另一個的面數,則稱這兩個正多面體是互為對偶正多面體,其...
- 對偶多面體
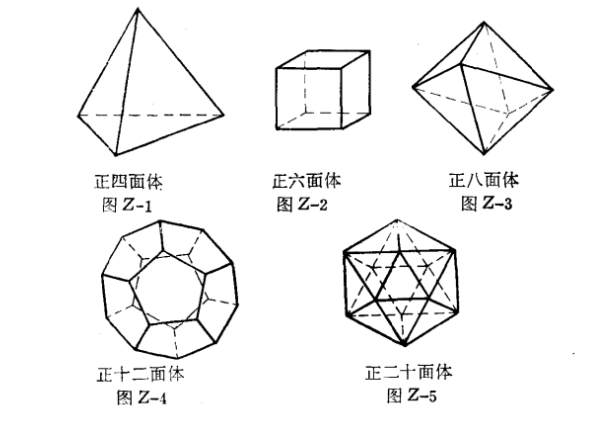
一個正多面體 一個正多面體和以它的各面中心為頂的正多面體,叫做互為對偶的正多面體。正六面體和正八面體是互為對偶的正多面體;正十二面體和正二十面體是互為對偶的正多面體;正四面體的對偶多面體是正四面體。根據對偶原則,每種多面體都存在對偶多面體。一種多面體的對偶多面體的對偶多面體等同該種多面體。對偶的...
- 多面體群
一個正多面體和以它的各面中心為頂的正多面體,叫做互為對偶的正多面體。由歐拉定理推出:凸正多面體只有五種,即:正四面體、正八面體、正二十面體、正六面體(正方體)、正十二面體,其中正四面體、正八面體和正二十面體的各面都是正三角形,正六面體的各面是正方形,正十二面體的各面是正五邊形。正六面體...
- 正十二面體
正十二面體是由12個正五邊形所組成的正多面體,它共有20個頂點、30條棱、160條對角線,被施萊夫利符號{5,3}所表示,與正二十面體互成對偶。它是一種只具有正四面體對稱性的五角十二面體的特殊形式,五角十二面體的另一種特殊形式是具有正八面體對稱性的卡塔蘭多面體菱形十二面體,它(加上所有其它的五角十二...
- 七面體
(4)五角柱的對偶是雙五角錐;(5)五角柱用威廉表示法可表示為:P5;(6)五角柱是凸多面體。正三角錐柱 正三角錐柱為92種Johnson多面體(J₇)中的其中一個,可由正多面體中的正四面體(正三角錐)與三角柱於相等大小的三角形面接合而組成。這92種Johnson立體最早在1996年由Johnson Norman命名並給予描述。Joh...
- 化學中的多面體
第2章 多面體幾何學 2.1 多面體概述 2.2 多邊形面 2.3 正多面體 2.4 半正多面體(Ⅰ)2.5 半正多面體(Ⅱ)2.6 半正多面體(Ⅰ)的對偶多面體 2.7 多面體模型的製作 參考文獻 第3章 化學中的四面體 3.1 概述 3.2 主族元素及其化合物結構中的四面體 3.3 過渡金屬元素化合物結構中的四面體 3.4 ...
- 九面體
九面體是指由9個平面組成的多面體,而邊長全部等長的九面體是七角柱是一種半正多面體。在九面體中,四角錐柱和它的對偶多面體都是九面體。九面體可以是七角柱、八角錐、雙三角錐柱等多面體。凸九面體 在所有凸九面體中,包含鏡射像共有2606種拓樸結構明顯差異的凸九面體。其中有8種具有7個頂點、74種具有...
- 十一面體
常見的十一面體有錐體和柱體、部分的詹森多面體和半正多面體,此處的半正多面體並非阿基米德立體,而是正九角柱。其他十一面體還有九角柱、十角錐、正五角錐反角柱的對偶、雙對稱十一面體等多面體,其中雙對稱十一面體可以密鋪空間。截半三角柱 在幾何學中,截半三角柱是指經過截半變換後的三角柱,是一種十一面體,其...
- 十面體
八角柱是一種底面為八邊形的柱體,由10個面24條邊和16個頂點組成。正八角柱代表每個面都是正多邊形的八角柱,其每個頂點都是2個正方形和1個八邊形的公共頂點,因此具有每個角等角的性質,可以歸類為半正十面體。九角錐 九角錐是一種底面為九邊形的錐體,其具有10個面、18條邊和10個頂點,其對偶多面體是...
- 內側三角六邊形二十面體
內側三角六邊形二十面體是一種凹多面體,屬於星形多面體,是為雙三斜十二面體,U41的對偶多面體。它有20個面,每個面都是的等角的凹六邊形。它有24個頂點:12個在外部和12在內部。它有60個邊緣。不像大三角六邊形二十面體,內側三角六邊形二十面體再拓撲結構上來說是一個索引為二的正多面體可透過扭曲三角成正...
- 十五面體
十五面體是指具有十五個面的多面體。在
- 正二十面體
正二十面體(Regular icosahedron) 是由20個等邊三角形所組成的正多面體,共有12個頂點,30條棱,20個面。為五個柏拉圖多面體之一。定義 正多面體各個面都是全等的正多邊形,並且各個多面角都是全等的多面角。其中面數最少的是正四面體,面數最多的是正二十面體。正二十面體(Regular icosahedron) 是由20個等邊三角...
- 卡塔藍多面體
卡塔藍多面體 卡塔藍多面體是2016年公布的化學名詞。 定義 與13種阿基米德多面體相對應的13種對偶多面體。卡塔藍多面體是由一種形狀的多邊形面組成,且多面體的面都不是正多邊形面,它們不屬於半正多面體。 出處 《化學名詞》。
- 二維、三維歐式幾何的對偶原理
2.8“黃正多面體”2.9點、線、面之間的簡單關係 2.10基本作圖 2.11“黃異面直線”2.12“黃線段”2.13“黃角”2.14“黃二面角”2.15“黃三角形”2.16“黃三面角”2.17“黃三角形”的“重心”2.18“黃三角形”的“內心”2.19“黃三角形”的“垂心”2.20“黃微點幾何”2.21“升維”和“降維”2...
- 截角二複合正四面體
截角二複合正四面體 截角二複合正四面體,是一種凹多面體,屬於星形多面體, 也是一中半正多面體的均勻複合體,外觀看起來像兩個截角四面體卡在一起,或是截去頂點的星形八面體。從其考克斯特記號可以看出:該複合體表示的兩個對偶中,其中一個位置與截角交錯正方體相關,其在考克斯特記號中以表示。
- 四稜柱
在幾何學中,四角柱又稱四稜柱,是指底面為四邊形的柱體,當底面為正方形時可成為正六面體。所有四角柱都有6個面8個頂點和12個邊。對偶多面體是雙四角錐。概念 稜柱的底面:稜柱中兩個互相平行的面,叫做稜柱的底面。四稜柱: 底面為四邊形的稜柱是四稜柱。斜四稜柱:側棱不垂直於底面的四稜柱叫做斜四...
- 正二十四胞體
它的施萊夫利符號為{3,4,3},自身對偶 其頂點圖是立方體,正24胞體每條棱上有3個正八面體。三維投影 施萊格爾投影 嚴格來說正二十四胞體是沒有三維類比的,因此也不好說是根據哪個正多面體的施萊格爾投影類比到三維上來的。不過只要根據正二十四胞體每條棱上有3個正八面體這個條件在三維空間上畫投影就不會太難...
熱門詞條