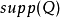設F是任意域;以0,1分別表示它的零元和乘法單位元。若-1不能表作F中的平方和,就稱F為實域(或者形式實域)。常見的有理數域Q和實數域R,都是這個意義下的實域;但複數域C以及有限域,都不是實域。
基本介紹
- 中文名:實域
- 外文名:real field
- 別名:形式實域
- 所屬學科:數學
- 所屬問題:域論(序域)
基本介紹,相關概念與定理,
基本介紹
實域(real field)亦稱形式實域,是與序域密切相關的一種域。一個域F,若在其中不存在形式如
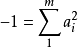

相關概念與定理
對於F中任何子集P,今規定以下記法

定義1 設P為F的子集,如果滿足條件:
(1)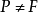 ;
;
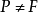
(2) ; (1)
; (1)

(3) ,
,

則稱P是F的一個正錐。
當P是F的正錐時,從上述條件不難得知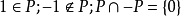 ;以及對於任何
;以及對於任何 ,皆有
,皆有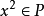 。從F的正錐P,可以定出F中一個二元關係
。從F的正錐P,可以定出F中一個二元關係 如下:
如下:
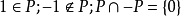

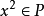



從(1)式可知 應滿足以下的條件:
應滿足以下的條件:

(1) ;
;

(2) 對於任何二元素 ,必有
,必有 ,或者
,或者 ;
;



(3) 由 和
和 ,得到
,得到 ;(3)
;(3)



(4) 由 和
和 ,得到
,得到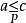 ;
;


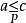
(5) 由 有
有 ;
;


(6) 由 和
和 ,得到
,得到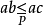 。
。


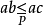
當 與
與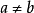 同時成立時,我們簡記作
同時成立時,我們簡記作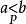 。
。

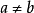
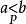
如果以P記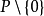 ,則
,則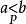 若且唯若
若且唯若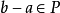 。
。
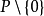
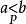
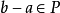
我們稱≤為P所定的序關係。一般而言,任何一個定義在F上,且滿足(3)的二元關係≤,都可稱作F的序關係。當給定了F的一個序關係≤,我們也可以反過來在F上定出正錐。令



一個在其中可以定出序的域,稱作可序的,或者可序域,可序域一般可以有許多序,當我們特別取定F的某個序P時,就稱F為序域,記以(F,P),或者(F,≤)。在可序域中,不同的序之間,不存在集包含關係(作為正錐而言)。這是下述引理所指出的:
引理1 設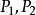 是F的兩個序,若有
是F的兩個序,若有 ,則套用
,則套用 。
。
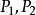


命題1 可序域必定是實域;可序域的特徵只能是0。
為了進一步闡明可序域與實域的關係,現在再引進一個概念:
定義2 設Q是F的一個子集。若有:
(1)  ;
;

(2) ; (4)
; (4)

(3)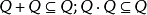 ;
;
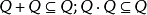
則稱Q是F的一個亞正錐,或者說,Q給出F的一個亞序。
以下為簡便計,也逕稱Q為F的亞序;此時又稱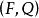 為一個亞序域。從定義立即知道
為一個亞序域。從定義立即知道 ;並且,亞序域是實域,反之,當F是實域時,
;並且,亞序域是實域,反之,當F是實域時, ;此時
;此時 ;滿足條件(4)。因此,
;滿足條件(4)。因此, 是F的一個亞序,又按集包含關係,
是F的一個亞序,又按集包含關係, 是最小的亞序,所以也稱作F的弱亞序。實域,可以作為亞序域
是最小的亞序,所以也稱作F的弱亞序。實域,可以作為亞序域 。
。
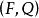






與序的情形不同,在實域的亞序之間,可以有集包含關係存在,今有:
引理2 F中按集包含關係的極大亞序,就是F的一個序。

命題2 實域一定是可序的。
由命題1和2,即得:
定理1 F成為實域,若且唯若F是個可序域。
引理2 尚可作進一步的強化如下:
引理3設(F,Q)是個亞序域,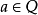 。於是存在F的某個序P,使得有
。於是存在F的某個序P,使得有 ,以及
,以及 。
。
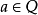


我們稱滿足 的序P為亞序域(F,Q)的一個序,從上述引理立即得到:
的序P為亞序域(F,Q)的一個序,從上述引理立即得到:

定理2 對於亞序域(F,Q),等式

由於實域F可作為亞序域 ,故有
,故有

推論(阿廷定理) 對於實域F,等式
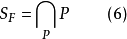
在序域(F,P)中,可以引入一些與通常相類似的概念,對於元素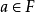 ,今規定它的絕對值
,今規定它的絕對值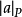 ,如下
,如下
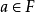
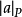
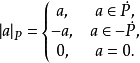


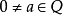
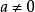
最後還應指出,(6)的左邊對於任何域都是有意義的。如果F不是實域,同時它有特徵≠2,則任何 都可以表如
都可以表如

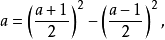

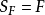
把序和亞序的概念推廣到交換環上,現在設A是一個帶有單位元素1的交換環;以 記A中由所有的有限平方和所成的子集,與域的情形一樣,我們稱A中滿足定義2的子集Q為A的一個亞正錐,或者逕稱作A的亞序,當
記A中由所有的有限平方和所成的子集,與域的情形一樣,我們稱A中滿足定義2的子集Q為A的一個亞正錐,或者逕稱作A的亞序,當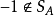 時,
時, 本身就是A的一個亞序。這個亞序也稱作A的弱亞序,就環的情形而論,今有一個與引理2相類似的結論:
本身就是A的一個亞序。這個亞序也稱作A的弱亞序,就環的情形而論,今有一個與引理2相類似的結論:

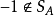

引理4 對於A的任何一個給定的亞序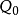 ,必然存在亞序Q,滿足
,必然存在亞序Q,滿足 ,以及
,以及
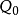


根據這個引理,我們把滿足上式的亞序稱作交換環A的序;又稱素理想J為序Q的支柱,記作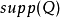 。於是得到了:
。於是得到了: