基本介紹
密率作為中國古算名
 祖沖之
祖沖之密率作為數論中的概念
基本介紹


 祖沖之
祖沖之
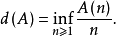
密率有兩種含義,一個是指中國古算名,祖沖之發現的圓周率的分數近似值π≈355/113,稱為密率,它是相對於約率π≈22/7而言的;還有一個含義是指數論中的一個...
漸近密率是一個與密率近似的概念。若集合A是以r(正整數)為公差的等差數列,則δ*(A)=1/r;若集合A是由等比數列所組成,則其漸近密率為0;所有完全平方數所...
外切密率(Waiqie milu )《求表捷術》中的一種.四卷,清戴煦撰,成書於1852年.該書論述了以前中國數學家未曾討論過的正切、餘切、正割、餘割等四種三角函式的...
南北朝時祖沖之算出的圓周率的近似值在3.1415926和3.1415927之間,並提出圓周率的疏率(或作約率)為22/7,密率為355/113。祖沖之首創上下限的提法,將圓周率規定在...
周伯壎,男,祖籍湖南。數學家。長期從事數論、代數方面的教學與研究。在史尼雷爾曼密率理論、循環群與環論研究方面頗有建樹。是在我國開展同調代數與代數K理論研究的...
割圓連比例是清代級數理論的幾何學基礎,最先由明安圖在《割圜密率捷法》中闡明,其後經項名達、董祐誠等數學家的工作而趨於完善。。割圓連比例的中心問題是已知...
萬曆二十四年(1596年),朱載堉完成《律呂精義》(內外篇)一書,提出了“新法密率”。這是中國音樂史上一件具有劃時代意義的事件,也成為人類文化史上最早出現的...
都是挑戰。例如,我國古代數學家祖沖之指出,分數355/113是圓周率π的一個很好的近似值,稱之為密率。密率好在哪?這是一個不錯的科普話題。數學大師華羅庚指出,在...
第一篇介紹數論中幾種重要的初等方法,包括шhиpeльmah的密率論及由此發展而成的漸近密率與本性分量的理論,brun的篩法與更精密的selberg篩法,素數定理的初等...
