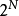DMRG 的起源
從數值計算的角度來看,量子多體物理主要的困難之處就在於系統的
希爾伯特空間維度隨著系統的尺寸呈指數成長,例如,一個由N個
自旋1/2的粒子所組成的一維晶格系統其
希爾伯特空間維度大小為
。 傳統的解決方法有兩種:
基於數值重整化群(Numerical Renormalization Group,簡稱NRG)的重整化方法,可以計算很大的系統。重整化的一般思想是:減少系統的自由度,並在這個縮減的空間中,通過特定的重整化技巧,在疊代過程中保持系統的自由度數不變,並使約化系統最終收斂到真正系統的低能態中。然而,NRG一般只適用在雜質系統中,當演算一般的格點系統,如赫巴德模型(Hubbard model)時,往往出現很大的誤差。
史提芬·懷特最先意識到,NRG在演算Hubbard模型中的失敗,是由於在NRG的疊代過程中忽略了環境對系統的影響。換句話說,NRG的重整化方法——只保留低能量本徵態——並不能正確得出下一次疊代時的低能狀態。
DMRG的重整化方法不同於NRG。DMRG在重整化前,把整個系統視為兩個部分,一部分為
系統,一部分為
環境,而
系統和
環境的整體稱為
超塊。接著,計算
超塊的基態,有了基態之後便計算
約化密度矩陣,然後
對角化這個
約化密度矩陣,選出擁有較大的本徵值的本徵態。這些擁有較大的本徵值的本徵態正是基態性質最重要的態,然後根據此標準對
系統部分做重整化。
實行DMRG的技巧
實際實行DMRG是一個很冗長的工作,一些主要常用的計算手段如下:
為了得到
超塊的
基態,通常利用Lanczos 算法或Jacobi-Davidson 算法來
對角化超塊的
哈密頓算符。
一般的情況下,Lanczos 算法需要一個初始的隨機
向量。通過若干次疊代後,該
向量收斂到
基態。這說明算法的計算速度跟
向量疊代到
基態的次數有關。顯然,如果能找出一個跟
基態非常接近的
向量做初始的隨機
向量,Lanczos 算法的效率必然大大提高。史提芬·懷特在公元1996年提出:透過
波函式轉換可將目前這次計算得到的
基態,作為下一次Lanczos 算法的初始
向量。如此一來便加速
對角化超塊的
哈密頓算符所花的時間。
Lanczos 算法中需要做被
對角化矩陣和
向量的乘積計算。該被
對角化的矩陣往往非常大,直接列出該矩陣和做矩陣向量乘積會嚴重降低Lanczos 算法效率。當該被
對角化矩陣可以拆分為幾個小矩陣的
直積之和時(DMRG所計算的格點系統往往有這種性質),可以無需直接寫出該矩陣而完成整個Lanczos 算法。
如缺少上述的一些計算手段,DMRG可能難以完成對實際物理模型的演算。
套用
DMRG 已經成功的在許多不同的一維模型上計算低能態的一些性質,如易辛模型,海森保模型等自旋模型,
費米子系統如Hubbard 模型,雜質系統如
近藤效應,
玻色子系統,混合
玻色子與
費米子的系統。隨著現代電腦硬體技術的進步,DMRG套用在二維系統上可行性愈來愈高,目前一般的作法是將二維系統視為一個
多腿的梯子,再將梯子的長度拉長。2011年發表在《Science》封面的一篇文章中,利用 DMRG 探討二維Kagome晶格中的自旋-1/2系統的基態。由這篇文章來看, DMRG 可能仍是對付二維系統最強大的武器。
DMRG 的擴充
DMRG的巨大成功帶給人們許多衝擊與啟示,可惜的是由於
波函式被表示成
矩陣積態(Matrix Product State),造成DMRG在處理二維量子晶格系統時特別困難,更別說是三維的量子系統。繼承DMRG的知識和技術,許多物理學家著手發展適合研究二維甚至三維系統中的數值方法,例如:TEBD(Time-evolving block decimation)、PEPS(Projected Entangled Pair States)、MERA(multi-scale entanglement renormalization ansatz),等等。另一方面,也有許多物理學家在原有的DMRG方法上加以改良,讓科學家可以處理更多有趣的一維量子晶格系統的問題,例如:時間演化、有限溫度,等等。
其他
強關聯繫統中常見的數值方法還有:量子蒙特卡羅法(Quantum Monte Carlo)、
精確對角化法(Exact Diagonalization)。
一個密度矩陣重整化群的實例:海森堡模型的DMRG