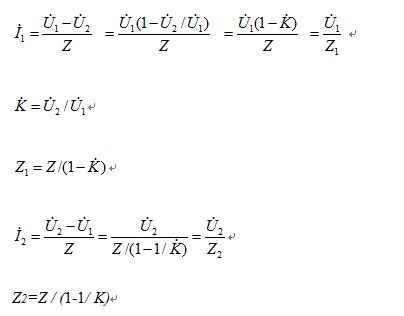設有一個具有n個節點的線性電路,其中節點0為參考點。而節點1和節點2之間有一阻抗Z相接,如圖1所示。又設節點電位U1和U2的比值為一常數K,即U2/U1=K。現在把Z從節點1和節點2之間移去,在節點1與參考節點0之間接另一個阻抗Z1,在節點2與參考節點0之間接另一個阻抗Z2,如圖2所示。如果Z1=Z/(1-K),Z2=Z/(1-1/K),則圖1、2所示兩電路,就各節點的KCL方程來說是完全等效的。這就是密勒定理。
基本介紹
- 中文名:密勒定理
- 外文名:miller theorem
- 套用學科:物理
- 適用領域範圍:電路