容量維(capacitydimension)亦稱容積維或柯爾莫哥洛夫維一種分數維數.它與豪斯多夫維數相近,有不同定義方法.
詳情
給定一個點集x,N(s)是能夠覆蓋x的直徑為C的小球的最小數目,如果存在有限極限
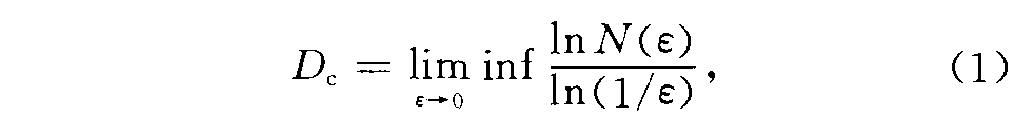
則D。稱為x的容量維.與豪斯多夫維數定義相比較,容量維定義的式子中僅多了一項inf,而在大多數實際計算中,兩者是相同的.基於此項事實,有時它們甚至被認為是一個維數,即豪斯多夫維數.與容量維類似的維數定義,還有豪克斯(Hawks , J.)於 1974年引人的上嫡維數,其定義是將式(1)中的inf

豪克斯證明了對於大多數情形,DH=D}=Do.柯爾莫哥洛夫(KOJIMOPOpOB } A. H.)於1959年曾提出過另一形式相近的分維,其定義是:給定一個點集二,記 M2P,若存在有限極限
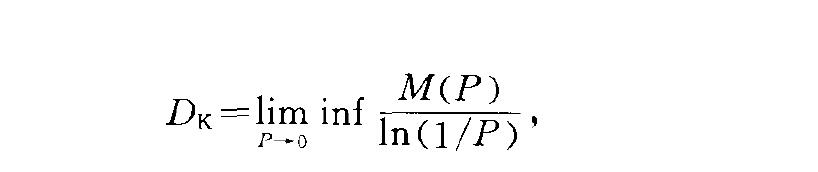
則DK為集x的另一形式的分維.DK與DO(豪斯多夫維數)相差不大.實際上,對於線段上的點集而言, M(P>=N(P>,因此DK=D}.11 由於上面定義的三種分數維數均與豪斯多夫維數相差不大,因此,一般把它們視為豪斯多夫維數的同類,有些文獻甚至把它們視為相同一般地,它們之間存在下述關係:

