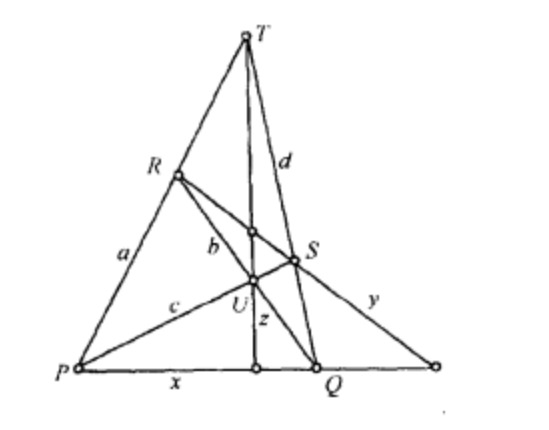
完全n線形(complete n-side)是一種簡單的平面圖形,是由平面上的n條直線(n≥3,其中無三線共點)及它們每兩條直線的交點所組成的平面圖形。這n條直線稱為完全n線形的邊,n(n-1)/2個交點稱為完全n線形的頂點,完全n線形的對偶圖形是完全n點形。
基本介紹
- 中文名:完全n線形
- 外文名:complete n-side
- 所屬學科:數學
- 所屬問題:高等幾何(射影幾何)
- 舉例:完全三線形、完全四線形等
基本介紹


舉例說明
名稱 | 完全四點形ABCD | 名稱 | 完全四線形abcd |
頂點 | A,B,C,D (4個) | 頂點 | P,Q; R,S; T,U axc,bxd;axb,cxd;axd,bxc(6個) |
邊 | p,q;r,s;t,u AC,BD;AB,CD;AD,BC(6條) | 邊 | a,b,c,d (4條) |
對邊 | 沒有公共頂點的邊 p,q;r,s;t,u (3組) | 對頂 | 不在同一條邊上的頂點。 P,Q; R,S; T,U (三組) |
對邊點 | 對邊的交點 X, Y, Z pxq; rxs; txu (3個) | 對頂線 | 對頂的連線 x, y, z PQ; RS; TU (3條) |
對邊三點形 | 三點形XYZ | 對頂三角形 | 三線形xyz |
完全四點形和完全四線形的調和性質
完全四點形上不通過同一個頂點的兩條邊叫做對邊。有三對:(圖1)AB和CD,AD和BC,AC和BD。每對對邊的交點叫做對角點。有三個:L,M,N。它們構成一個對角三點形。對角點的連線叫做對角線。有三條:LM,MN,NL。 | 完全四線形上不在同一條邊上的兩個頂點叫做對頂點。有三對:(圖2)a×b和cxd,a×d和b×c,a×c和bxd,每對對頂點的連線叫做對角線。有三條:l,m,n。它們構成一個對角三線形。對角線的交點叫做對角點。有三個:lxm,m×n,n×l。 |
定理1 設E是一個完全四點形ABCD的對角點ACxBD,且P,Q是另外兩個對角點。則(EP,EQ;AC,BD)=-1。 | 定理1' 設e是一個完全四線形abcd的對角線(axc)x(bxd)。且p,q是另外兩條對角線。則(exp,exq;axc,bxd)=-1。 |