定義 如果一個數恰好等於它的真因子之和,則稱該數為“完全數”。各個小於它的
約數 (真約數,列出某數的約數,去掉該數本身,剩下的就是它的真約數)的和等於它本身的自然數叫做完全數(Perfect number),又稱完美數或完備數。
例如:第一個完全數是6,它有約數1、2、3、6,除去它本身6外,其餘3個數相加,1+2+3=6。第二個完全數是28,它有約數1、2、4、7、14、28,除去它本身28外,其餘5個數相加,1+2+4+7+14=28。第三個完全數是496,有約數1、2、4、8、16、31、62、124、248、496,除去其本身496外,其餘9個數相加,1+2+4+8+16+31+62+124+248=496。後面的完全數還有8128、33550336等等。
特有性質 (1)所有的完全數都是
三角形數 。一定數目的點或圓在等距離的排列下可以形成一個等邊三角形,這樣的數被稱為
三角形數 。例如:6=1+2+3;28=1+2+3+4+5+6+7;496=1+2+3+...+30+31;8128=1+2+3…+126+127。
(2)所有的完全數的倒數都是調和數。例如:1/1+1/2+1/3+1/6=2;1/1+1/2+1/4+1/7+1/14+1/28=2;1/1+1/2+1/4+1/8+1/16+1/31+1/62+1/124+1/248+1/496=2。
(3)可以表示成連續奇
立方數 之和。除6以外的完全數,都可以表示成連續奇立方數之和,並規律式增加。例如:28=1+3^3;496=1^3+3^3+5^3+7^3;8128=1^3+3^3+5^3+……+15^3;33550336=1^3+3^3+5^3+……+125^3+127^3。
(4)都可以表達為2的一些連續正整數次冪之和。不但如此,而且它們的數量為連續質數。例如:6=2^1+2^2;28=2^2+2^3+2^4;496=2^4+2^5+2^6+2^7+2^8;8128=2^6+2^7+2^8+2^9+2^10+2^11+2^12;33550336=2^12+2^13+……+2^24。
(5)完全數都是以6或8結尾。如果以8結尾,那么就肯定是以28結尾。(科學家仍未發現由其他數字結尾的完全數。)
(6)各位數字輾轉式相加個位數是1。除6以外的完全數,把它的各位數字相加,直到變成個位數,那么這個個位數一定是1。例如:28:2+8=10,1+0=1;496:4+9+6=19,1+9=10,1+0=1;8128:8+1+2+8=19,1+9=10,1+0=1;33550336:3+3+5+5+0+3+6=28,2+8=10,1+0=1。
(7)它們被3除餘1、被9除餘1、1/2被27除餘1。除6以外的完全數,它們被3除餘1,9除餘1,還有1/2被27除餘1。28/3 商9餘1,28/9 商3餘1,28/27 商1餘1。496/3 商165餘1,496/9 商55餘1。8128/3 商2709餘1,8128/9 商903餘1,8128/27 商301餘1。
歷史 公元前6世紀的
畢達哥拉斯 是最早研究完全數的人,他已經知道6和28是完全數。畢達哥拉斯曾說:“6象徵著完滿的婚姻以及健康和美麗,因為它的部分是完整的,並且其和等於自身。”有些《
聖經 》注釋家認為6和28是上帝創造世界時所用的基本數字,因為上帝創造世界花了六天,二十八天則是月亮繞地球一周的日數。
聖·奧古斯丁 說:6這個數本身就是完全的,並不因為上帝造物用了六天;事實上,因為這個數是一個完全數,所以上帝在六天之內把一切事物都造好了。
圖1 畢達哥拉斯
在中國文化里:有六穀、六畜、戰國時期的六國、秦始皇以六為國數、六常(仁、義、禮、智、信、孝)、天上四方有二十八宿等等,6和28,在中國歷史長河中,之所以熠熠生輝,是因為它是一個完全數。難怪生有的學者說,中國發現完全數比西方還早呢。
完全數誕生後,吸引著眾多數學家與業餘愛好者像淘金一樣去尋找。它很久以來就一直
對數 學家和業餘愛好者有著一種特別的吸引力,他們沒完沒了地找尋這一類數字。接下去的兩個
完數 看來是公元1世紀,
畢達哥拉斯學派 成員尼克
馬修斯 發現的,他在其《
數論 》一書中有一段話如下:也許是這樣,正如美的、卓絕的東西是罕有的,是容易計數的,而醜的、壞的東西卻滋蔓不已;是以
盈數 和虧數非常之多,雜亂無章,它們的發現也毫無系統。但是完全數則易於計數,而且又順理成章:因為在個位數里只有一個6;十位數里也只有一個28;第三個在百位數的深處,是496;第四個卻在千位數的尾巴頸部上,是8128。它們具有一致的特性:尾數都是6或8,而且永遠是偶數。但在茫茫數海中,第五個完全數要大得多,居然藏在千萬位數的深處!它是33550336,它的尋求之路也更加
撲朔迷離 ,直到十五世紀才由一位無名氏給出。這一尋找完全數的努力從來沒有停止。電子計算機問世後,人們藉助這一有力的工具繼續探索。
笛卡爾 曾公開預言:“能找出完全數是不會多的,好比人類一樣,要找一個完美人亦非易事。”時至今日,人們一直沒有發現有奇完全數的存在。於是是否存在奇完全數成為數論中的一大難題。只知道即便有,這個數也是非常之大,並且需要滿足一系列苛刻的條件。
圖2 數論論著
疑難問題 (1)到底有多少完全數?
答:尋找完全數並不是容易的事。經過不少數學家研究,到2018年為止,一共找到了51個完全數。
(2)有沒有奇完全數?
答:奇怪的是,已發現的51個完全數都是偶數,會不會有奇完全數存在呢?如果存在,它必須大於10^300。至今無人能回答這些問題。儘管沒有發現奇完全數,但是當代數學家奧斯丁·歐爾證明,若有奇完全數,則其形式必然是12^p+1或36^p+9的形式,其中p是
素數 。在10^300以下的自然數中奇完全數是不存在的。
另外,如果存在奇完全數,則它們必能表示p^2*q的形式,除6外的偶完全數亦有此性質。
計算方法 推導公式 大數學家
歐拉 曾推算出完全數的獲得公式:如果p是
質數 ,且2^p-1也是質數,那么(2^p-1)X2^(p-1)便是一個完全數。
例如p=2,是一個質數,2^p-1=3也是質數,(2^p-1)X2^(p-1)=3X2=6,是完全數。
例如p=3,是一個質數,2^p-1=7也是質數,(2^p-1)X2^(p-1)=7X4=28,是完全數。
例如p=5,是一個質數,2^p-1=31也是質數,(2^p-1)X2^(p-1)=31X16=496是完全數。
但是2^p-1什麼條件下才是質數呢?事實上,當2^p-1是質數的時候,稱其為
梅森素數 。到2013年2月6日為止,人類只發現了48個梅森素數,較小的有3、7、31、127等。
計算機枚舉法 例如:
(1)利用VB編程求10000以內完全數。
Dim a as Integer,b as Integer,c as Integer #include<stdio.h> (3)利用java語言編程求10000以內完全數。
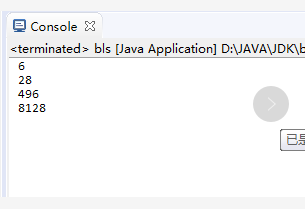
圖3Java代碼運行結果
public class test46 { (4)利用JavaScript語言編程求N以內完全數。
function perfectNumber(N){ 梅森素數 古希臘數學家
歐幾里得 在名著《
幾何原本 》中證明了素數有無窮多個,並論述完全數時提出:如果2^P-1是素數(其中指數P也是素數),則2^(P-1)(2^P-1)是完全數。
瑞士 數學家和物理學家
歐拉 證明所有的偶完全數都有這種形式。因此,人們只要找到2^P-1型素數,就可以發現偶完全數了。數學界將2^P-1型素數稱為“梅森素數”(Mersenne prime),因為法國數學家和
法蘭西科學院 奠基人
梅森 在這方面的研究成果較為卓著。梅森素數貌似簡單,但探究難度卻極大。它不僅需要高深的理論和純熟的技巧,而且還需要進行艱巨的計算。到2018年為止,人類僅發現51個梅森素數。
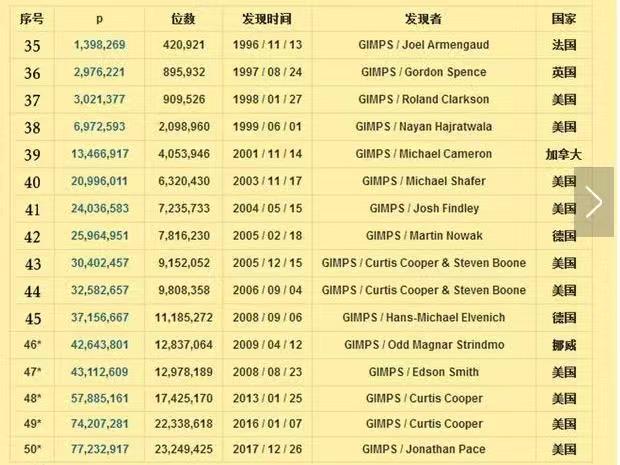
圖4 梅森素數表
值得提出的是:在梅森素數的基礎研究方面,法國數學家魯卡斯和美國數學家雷默都做出了重要貢獻;以他們命名的“魯卡斯-雷默方法”是已知的檢測梅森素數素性的最佳方法。此外,中國數學家和語言學家
周海中 給出了
梅森素數分布 的精確表達式,為人們尋找梅森素數提供了方便;這一研究成果被國際上命名為“
周氏猜測 ”。
梅森素數表如圖4所示。
已發現完全數 1……6
2……28
3……496
4……8,128
5……33,550,336
6……8,589,869,056
7……137,438,691,328
8……2,305,843,008,139,952,128
9……2,658,455,991,569,831,744,654,692,615,953,842,176
10……191,561,942,608,236,107,294,793,378,084,303,638,130,997,321,548,169,216
11……13,164,036,458,569,648,337,239,753,460,458,722,910,223,472,318,386,943,117,783,728,128
12……14,474,011,154,664,524,427,946,373,126,085,988,481,573,677,491,474,835,889,066,354,349,131,199,152,128
……
……
47 ……2^42643800 ×(2^42643801-1)
48 ……2^57885160 × (2^57885161-1)
由於後面數字位數較多,例子只列到12個,第13個有314位。
到第39個完全數有25674127位數,據估計它以四號字打出時需要一本字典大小的書。