在推導流體的控制方程時，可以從四種流動模型（空間位置固定的有限控制體、隨流體運動的有限控制體、空間固定的無限小控制體、隨流體運動的無窮小控制體）中推導出流體運動的控制方程。當流體穿越虛構的空間界面時（即控制體位置固定），對這個體積內的流體進行數學描述，得到的方程就是守恆型的方程。這裡假設的控制體是有限體積，包含了許多流體微團，稱得到的方程為積分形式的守恆型方程。如果空間縮小為流體微團大小，稱得到的方程為微分形式的守恆型方程。
基本介紹
- 中文名：守恆型方程
- 外文名：Conservation equation
- 套用領域：計算流體力學
簡介,流體運動的守恆型方程,
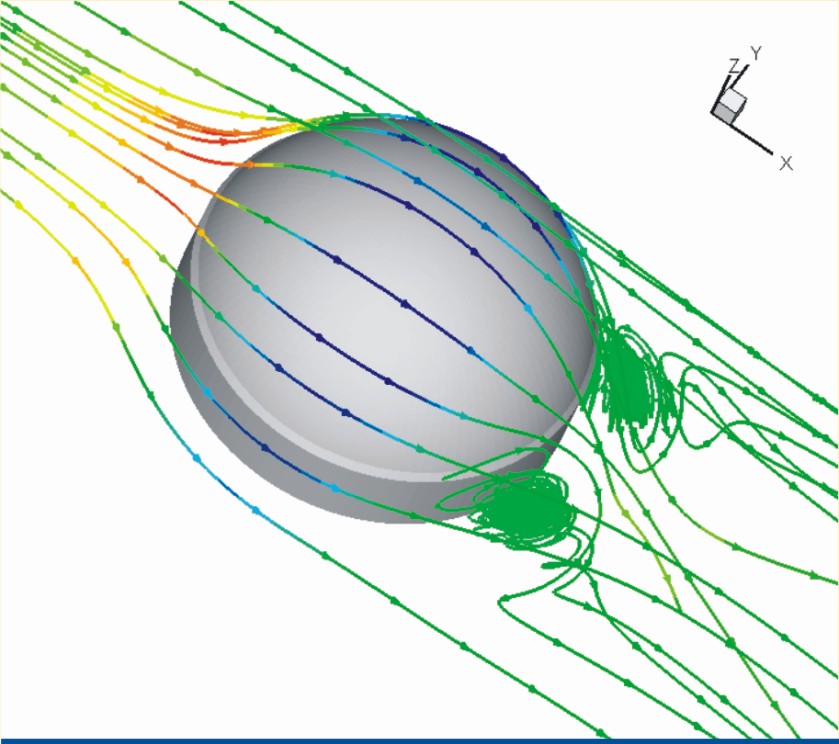
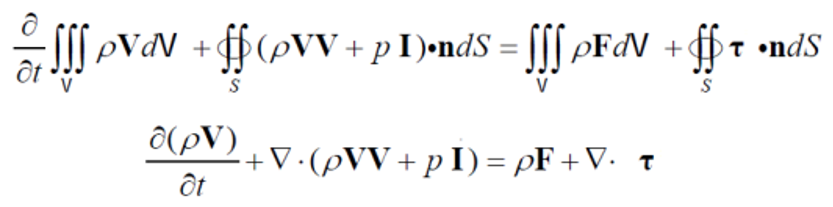簡介
在經典力學範疇內，任何流體運動的規律都是由以下牛頓三個基本定律為基礎的：(1)質量守恆定律；(2)牛頓第二定律：動量定理；(3)能量守恆定律。這三個基本定律可由積分/微分形式的數學方程組來描述。計算流體力學(CFD,Computationnal Fliud Dynamics)的核心任務就是通過數值離散方法把這些方程求解出來，從而得到流場在離散的時間/空間點上的數值解。
我們首先在流場中劃分一個有限大小的空間，這個空間是虛構的，存在以下兩種情況：
①這個空間是固定的。當流體穿越虛構的空間界面時，我們對這個體積內的流體進行數學描述，得到的方程就是守恆型的方程。這裡假設的空間大小是有 限體積，包含了許多流體微團，稱得到的方程為積分形式的守恆型方程。如果空間縮小為流體微團大小，稱得到的方程為微分形式的守恆型方程。
②這個空間隨流體一起運動。流體不能穿越這個虛構空間的界面，空間內的流體微團不能與外界交換。此時微團的性質隨空間位置的不同而不同，虛構空間的體積也會發生變化。同上，對於有限體積，得到積分形式的非守恆型方程，對於流體微團，得到微分形式的非守恆型方程。
流體運動的守恆型方程
連續性方程
動量方程
能量方程
微分方程可由積分型方程在考慮到控制體的形狀的任意性後導出。上面的積分方程是在控制體在空間固定的特殊情況下得到的Euler型積分方程。Euler型積分方程直觀地反映了質量、動量的守恆關係，也稱為守恆型積分方程。對守恆型積分方程直接套用Gauss定理，並考慮到控制體形狀的任意性後得到的微分型方程稱為守恆型微分方程。
