在實際問題中,信號有一定的失真是可以容忍的。但是當失真大於某一限度後,信息質量將被嚴重損傷,甚至喪失其實際價值。要規定失真限度,必須先有一個定量的失真測度。
失真函式是人們根據實際需要和失真引起的損失、風險、主觀感覺上的差別大小等因素人為規定的。
基本介紹
- 中文名:失真函式
- 外文名:distortional function
- 所屬學科:通信技術
提出背景
定義及公式
關於說明
平均失真度

試驗信道
信息率
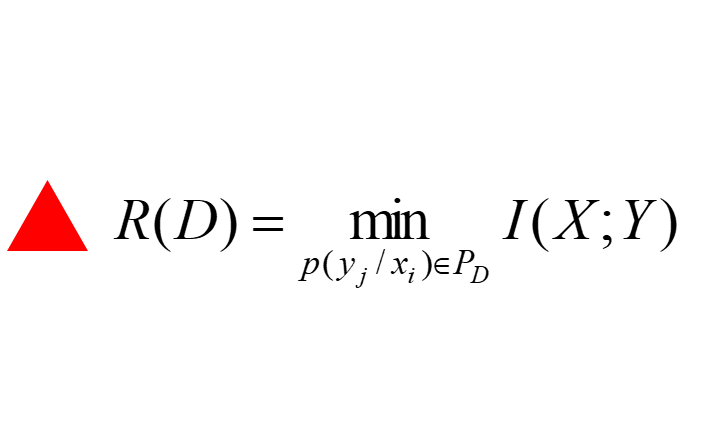

在實際問題中,信號有一定的失真是可以容忍的。但是當失真大於某一限度後,信息質量將被嚴重損傷,甚至喪失其實際價值。要規定失真限度,必須先有一個定量的失真測度。
失真函式是人們根據實際需要和失真引起的損失、風險、主觀感覺上的差別大小等因素人為規定的。

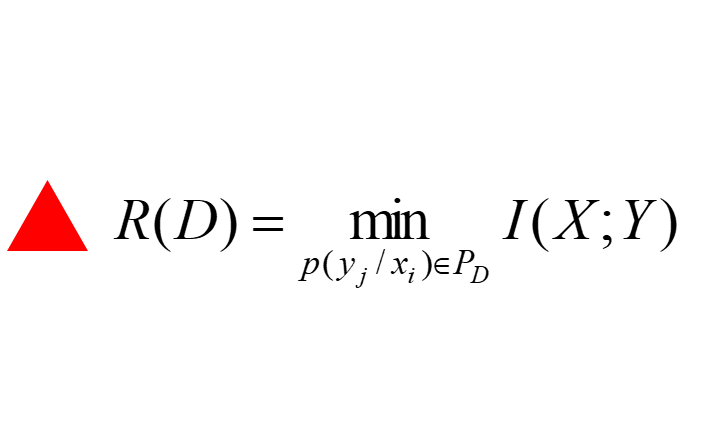
在實際問題中,信號有一定的失真是可以容忍的。但是當失真大於某一限度後,信息質量將被嚴重損傷,甚至喪失其實際價值。要規定失真限度,必須先有一個定量的失真測度。失真函式是人們根據實際需要和失真引起的損失、風險、主觀感覺上的差...
信息率失真函式(information rate distortionalfunction)信息理論的基本概念之一。在信源給定時,總希望在滿足一定失真的情況下信息傳輸率R儘可能小.即滿足D毛D‘時,尋找信息傳輸率R的下限值.從接收端看,即在D 全體可達率失真對於(R,D...
連續信源信息率失真函式(information ratedistortion function of continuous source)信息理論的一個基本函式。設連續信源U,其機率密度為p(u).接收端變數為V,信道傳遞機率密度為p (vu). U和V之間的失真函式為d<u,v,則平均失真度...
率失真函式和失真率函式(即率失真函式的反函式)是通過互信息的概念加以定義的。將編解碼器看成是一種信道,稱為試驗信道有條件機率P(y|x)。這一信道的輸入x和輸出y分別對應編碼的輸入和解碼的輸出。試驗信道輸入輸出間的互信息...
失真信息率函式 失真信息率函式(distortion rate function)是1993年公布的電子學名詞。公布時間 1993年,經全國科學技術名詞審定委員會審定發布。出處 《電子學名詞》第一版。
《非加性失真圖像隱寫研究》是依託深圳大學,由李斌擔任項目負責人的面上項目。項目摘要 基於最小化失真的圖像隱寫是信息隱藏的重要技術,設計失真函式是研究的熱點問題。在設計失真函式時考慮現實條件,使隱寫走出實驗室環境,具有重要的...
第5章限失真信源編碼 5.1失真函式 5.1.1失真度 5.1.2平均失真度 5.2信息率失真函式 5.2.1信息率失真函式的定義 5.2.2信息率失真函式的性質 5.2.3二進制信源的率失真函式 5.3信息率失真函式的計算 5.3.1...
《信息理論與編碼》以香農資訊理論為基礎,分兩大部分共8章向讀者系統介紹信息理論與編碼理論的基本思想:第一部分主要介紹了香農資訊理論的基本概念和性質,包括信息熵、信息率失真函式和信道容量,力求從基本概念上幫助讀者理解和掌握信息理論...
內容包括信息的統計度量;離散信源和連續信源;信道與信道容量;信源與信宿之間的平均失真度以及信息率失真函式;信源編碼與信道編碼;網路資訊理論基礎;資訊理論方法在信號處理中的套用。本書深入淺出,概念清晰,系統性強;可作為理工科高等...
系統介紹了資訊理論的3個基本概念(信源熵、信道容量和信息率失真函式),以及無失真信源編碼、限失真信源編碼、信道編碼和加密編碼中的理論知識及其實現原理。為了便於教學和加深對概念的理解,每章的*後還附有小結和習題。此外,本書配有...
第7章限失真信源編碼 7.1失真的度量 7.1.1失真函式和失真矩陣 7.1.2序列失真 7.1.3平均失真和保真度準則 7.2信息率失真函式 7.2.1信息率失真函式的定義和含義 7.2.2信息率失真函式的定義域和性質 7.2.3信息率失真函式和...
第6章 限失真信源編碼 171 6.1 失真測度 172 6.2 信息率失真函式及其性質 173 6.2.1 信息率失真函式的定義 173 6.2.2 信息率失真函式R(D)的性質 174 6.3 限失真信源編碼定理 178 6.4 離散信源信息率失真函式的計算 ...
本書系統地講述資訊理論與編碼的基礎理論,包含香農資訊理論的核心內容,全書共分7章,即緒論、信源與信息熵、信道與信道容量、信息率失真函式、信源編碼、信道編碼和加密編碼。本書文字通俗易懂,注重基本理論和實現原理,與實際通信系統緊密...
第6章 限失真信源編碼 6.1 引言 6.2 率失真函式的定義 6.2.1 失真函式 6.2.2 率失真函式的定義 6.3 率失真函式的性質 6.4 率失真函式的計算 6.5 連續信源的率失真函式 6.5.1 連續信源的率失真函式及其計算 6.5.2 ...
本書系統介紹和論述了信息的基本概念;資訊理論的起源、發展及研究內容;香農資訊理論的三個基本概念:信源熵、信道容量和信息率失真函式,以及與這三個概念相對應的三個編碼定理;解決通信系統有效性、可靠性和安全性的三類編碼:信源編碼、...
《資訊理論與編碼原理》系統地講述了資訊理論與編碼的基本理論,共11章,內容包括:信息的基本概念、信源及其信息量、信道及其容量、信息率失真函式、信源編碼和信道編碼定理、網路資訊理論以及信源編碼和信道編碼的理論與方法。除第1、5、7、...
包括信息的基本概念;資訊理論的起源、發展和研究內容;香農資訊理論的三個基本概念:信源熵、信道容量、信息率失真函式,以及與這三個概念相對應的三個編碼定理;解決通信有效性、可靠性和安全性的三類編碼:信源編碼、信道編碼和安全編碼—...
香農第三定理(保失真度準則下的有失真信源編碼定理)保真度準則下的信源編碼定理,或稱有損信源編碼定理。只要碼長足夠長,總可以找到一種信源編碼,使編碼後的信息傳輸率略大於率失真函式,而碼的平均失真度不大於給定的允許失真度,...
《信息理論與編碼》是一本人民郵電出版社出版的圖書,作者是呂峰。內容簡介 本書系統地講述了資訊理論的基礎理論。全書分8章,分別討論了信息的度量、信源無失真編碼、信道編碼、信息率失真函式、網路資訊理論以及信息安全的理論與方法。本書...
《信息理論與編解碼技術》論述了信息、信息系統和智慧型系統的概念與特性,信源和信道的分類,闡述了信源產生冗餘的根源,分析了去除冗餘的一般方法,重點論述了信源熵函式、信道容量代價函式和速率失真函式及其特性,給出了相應的信源編碼、...
第5章 限失真信源編碼 5.1 失真測度與信息率失真函式 5.1.1 平均失真度 5.1.2 信息率失真函式的定義 5.1.3 信息率失真函式的性質 5.2 信息率失真函式的計算 5.2.1 離散信源的率失真函式的計算 5.2.2 連續信源的率失真...
全書分7章,在介紹了有關信息度量的基礎上,重點討論了信道容量、率失真函式,以及無失真信源編碼、限失真信源編碼、信道編碼和密碼學中的理論知識及其實現原理在各章的最後還附有內容小結和大量習題,書後附有部分習題答案,便於讀者學習...
本書分9章,以信息熵為基本概念,以香農理論的3個基本定理為核心,系統地講述香農資訊理論的基本理論,主要內容包括離散信息和連續信息的度量、離散信道和連續信道的容量、無失真信源編碼定理、有噪信道編碼定理、信息率失真函式、信道編碼和...
全書共9章,內容包括:信息的定義和度量,離散信源和連續信源的信息熵,信道和信道容量,平均失真度和信息率失真函式,三個香農資訊理論的基本定理,若干種常見實用的無失真信源壓縮編碼的方法,以及信道糾錯編碼的基本內容和分析方法。本書...
《資訊理論與編碼》是由電子工業出版社於2006年7月1日出版的圖書,主編陳運。內容簡介 本書統論述香農資訊理論。主要介紹信息的定義、資訊理論的起源、發展及研究內容;香農資訊理論的三個基本概念,即信源熵、信道容量和信息率失真函式,以及與...
共有9章,內容包括:信息的定義和度量,離散信源和連續信源的信息熵,信道和信道容量,平均失真度和信息率失真函式,三個香農資訊理論的基本定理:無失真信源編碼定理、限失真信源編碼定理和信道編碼定理,若干種常見實用的無失真信源壓縮編碼...
4.3 限失真信源編碼原理 79 4.3.1 失真函式及保真度準則 79 4.3.2 信息率失真函式 83 4.3.3 信息率失真函式的定義域及性質 84 4.3.4 信息率失真函式的參量表述 88 4.3.5 離散信源信息率失真函式的計算 89 4.3.6 ...
而保真度準則下的信源編碼定理,或稱有損信源編碼定理,只要碼長足夠長,總可以找到一種信源編碼,使編碼後的信息傳輸率略大於率失真函式,而碼的平均失真度不大於給定的允許失真度。無線通信的實現勢必要解決兩大問題,其一是對信源進行...
第6章 限失真信源編碼 165 6.1 失真測度 165 6.2 信息率失真函式及其性質 167 6.2.1 信息率失真函式的定義 167 6.2.2 信息率失真函式的性質 168 6.3 限失真信源編碼定理 171 6.4 信息率失真函式的計算 171 ...
